Thorn Guide for the EHFinder Thorn

Original code and documentation by Peter Diener

\( \)Date\( \)

Abstract

This thorn locates the Event Horizon (EH) in an analytic or numerical spacetime by evolving a null surface backwards in time. The null surface is described at each time step as the 0-level iso-surface of a 3D scalar function \(f\). This level set description of the surface allows, trivially, changes of the topology of the surface so it is possible to follow the merger of two (or more) black holes into a final black hole.

1 Introduction

This thorn attempts to locate the Event Horizon (EH) in an analytic or numerical spacetime by evolving a null surface backwards in time. This method depends on the fact that, except in cases where the coordinates are adapted to outgoing null geodesics, an outgoing null surface started close to the EH, when evolved forward in time, is diverging exponentially from the EH. Reversing the time evolution then means that an outgoing null surface will converge exponentially to the EH. The level set function, \(f\), is evolved according to

\begin {eqnarray} \partial _{t}f & = & \frac {-g^{ti}\partial _{i}f+\sqrt {(g^{ti}\partial _{i}f)^{2}- g^{tt}g^{ij}\partial _{i}f\partial _{j}f}}{g^{tt}} \nonumber \\ & = & \beta ^{i}\partial _{i}f- \sqrt {\alpha ^{2}\gamma ^{ij}\partial _{i}f\partial _{j}f}, \label {AEIThorns_EHFinder_evolve} \end {eqnarray}

where in the second equation the lapse, shift and 3-metric has been substituted for the 4-metric. For more details on the theory and implementation see [1].

This thorn uses a level set description of the null surface, i.e.the surface is the 0-level isosurface of a 3D scalar function, \(f\), that is negative inside and positive outside the surface. With this choice of surface description one level-set function can describe multiple surfaces at the same time, simply by having several, disconnected regions with negative values. The biggest advantage, however, is that any change of topology of the surface is handled naturally and simply by the level-set function changing sign. Therefore this EHFinder can follow the EH during the merger of two (or more) black holes into one black hole.

To find the EH in a numerical spacetime several points have to be taken into consideration. Since the null surface has to be evolved backwards in time, the EHFinder has to be seen as a pre-processing analysis thorn. Therefore it is necessary to evolve the initial data forward in time while outputting enough 3D data, that the full 4-metric can be recovered at each timestep. The 3D data is then read back in, in reverse order, while the level-set function is evolved backwards in time. The thorn can evolve more than one level set function at a time using different initial guesses for the surfaces (NOTE: this is a quite recent feature and has not yet been tested extensively). More details about the actual use of the thorn in section 7

2 Re-initialization

The evolution equation for \(f\), equation (??), causes steepening of the gradient of \(f\), which is undesireble numerically. For that reason, \(f\) is periodically re-initialized to a distance function. That is, the values of \(f\) are changed so that the the value of \(f\) in a grid point is equal to the (signed) distance from the grid point to the surface \(f=0\). This is done by evolving \(f\) according to the following evolution equation (in the parameter \(\lambda \)) \begin {equation} \frac {df}{d\lambda } = -\frac {f}{\sqrt {f^{2}+1}}\left (|\nabla f|-1\right ) \label {AEIThorns_EHFinder_reinit} \end {equation} until a steady state is achieved. This method is called the pde-method since it is basically evolving a pde. Sometimes the \(f=0\) surface can be moved slightly during the re-initialization procedure. This happens when the surface develops a narrow neck just before a topology change. For that reason, there is an option to detect when this is about to happen and undo the re-initialization.

There used to be another method doing the re-initialization, but it proved inferior to the pde-method and was removed. Other methods may be implemented in the future.

3 The initial shape of the surface

Currently three different choices for the initial shape of the surface are implemented. The simplest choice is a sphere in which case \(f\) is set according to \begin {equation} f = \sqrt {(x-x_{0})^2+(y-y_{0})^2+(z-z_{0})^2} - r_{0}, \label {AEIThorns_EHFinder_sphere} \end {equation} where \(r_{0}\) is the radius of the sphere and \(x_{0}\), \(y_{0}\) and \(z_{0}\) are the coordinates of the center of the sphere. The second choice is a rotated and translated ellipsoid. The basic equation is here \begin {equation} f = \sqrt {\frac {x^{2}}{a^{2}}+\frac {y^{2}}{b^{2}}+\frac {z^{2}}{c^{2}}} - 1 \label {AEIThorns_EHFinder_ellipsoid} \end {equation} This ellipsoid is first rotated an angle \(\alpha \) around the \(z\)-axis, then rotated an angle \(\beta \) around the \(y\)-axis, then rotated an angle \(\gamma \) around the \(x\)-axis and finally the rotated ellipsoid is translated to have its “center” at the point \((x_{0},y_{0},z_{0})\). The final possible shape of the initial surface is an ovaloid of Cassini. This was implented initially to test changing the topology in flat space. it is most likely not useful for numerical data. In this case \(f\) is set according to \begin {equation} f = (x^{2}+y^{2}+z^{2})^{2} + a^{4} - 2 a^{2} (x^{2}-y^{2}-z^{2})-b^{4}. \label {AEIThorns_EHFinder_cassini} \end {equation} There are no translation or rotations implemented for the ovaloid of Cassini.

Different initial shapes can be used for the different level set functions used in the same run.

4 Excision

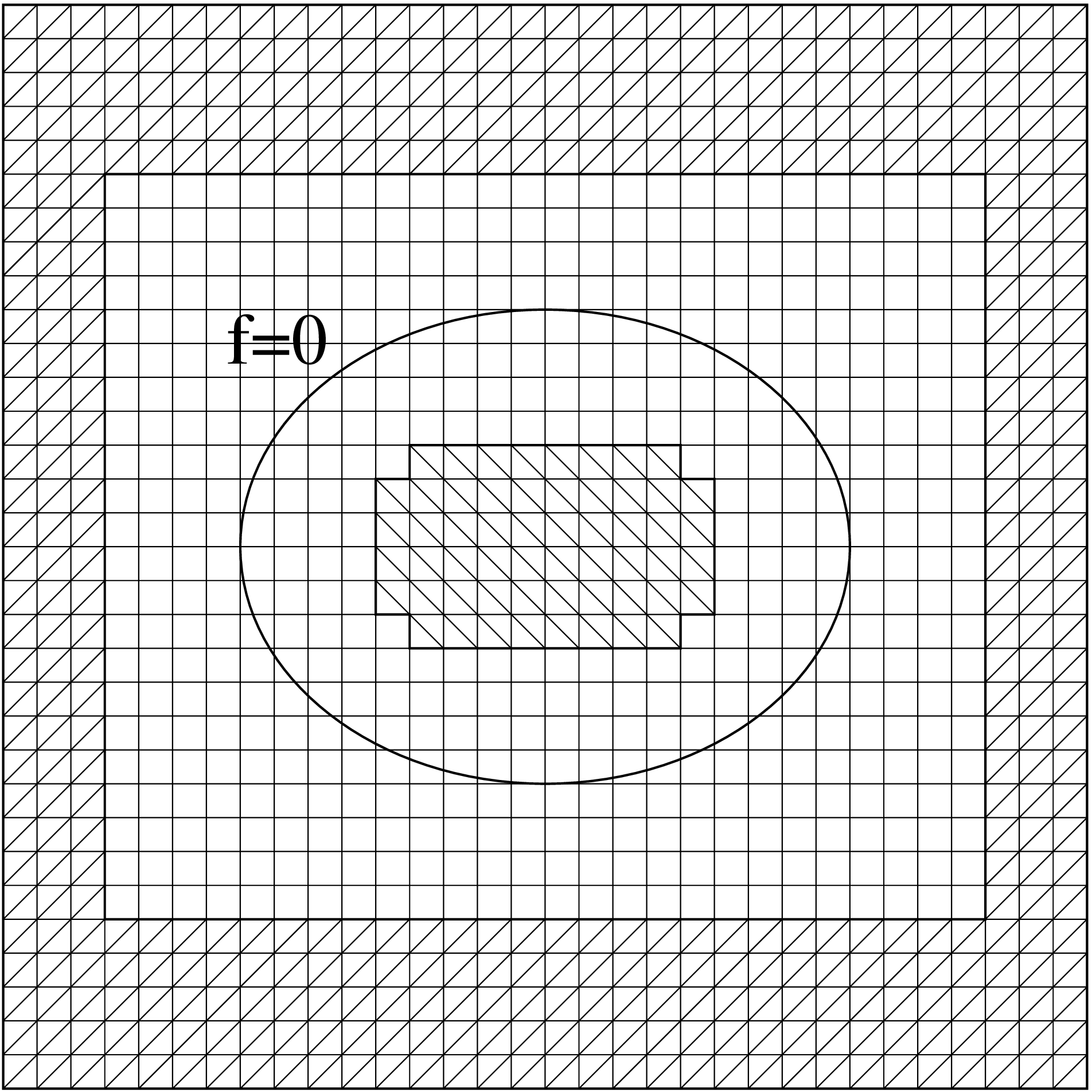
Even though the level set function, \(f\), in principle can be defined everywhere it is often advantageous to only evolve it in a certain region around the surface \(f=0\). Since \(f\) is re-initialized regularly to become a distance function, \(f\) itself can be used as a measure of the distance from a certain grid point to the surface \(f=0\). The parameter ehfinder::shell_width specifies the size of the active region around \(f=0\). However the interior and exterior excisions are handled differently. The interior excision is most simple, since here all grid points with \(f<-{\mbox {\tt ehfinder::shell\_width}}\) are marked as inactive. This should work in all cases when the excised region is everywhere concave, since then all points on the boundary of the excised region will have enough neighbouring active points to be able to calculate second order accurate one sided derivatives. If the interior excised region happens to have a convex region, this might fail. To avoid a similiar problem at the outer excised boundary, this boundary is shaped as a rectangular box. The box is chosen so that all points with \(f<{\mbox {\tt ehfinder::shell\_width}}\) are in the active region. This is illustrated in Figure 1, for the case

PIC


Figure 1: Illustration of the excision regions used internally by EHFinder. The hashed regions are excised.

ehfinder::shell_width = 4, where the excised regions are hashed.

Changes to the excision regions are only done after re-initialization, since it is only at this time that \(f\) is a distance function. The excision regions can move across the grid, tracking the surface \(f=0\).

Also if the numerical run was done with excision using SpaceMask, the EHFinder excision region is guaranteed to completely cover the numerical excision region. The EHFinder currently only supports the old style excision mask but the support of the new style excision mask should be trivial and fast to implement.

5 Upwinding

All finite differences used in the evolution of the null surface are second order one sided differences. For that reason a ghost_size larger or equal to 2 should always be used. It is possible to choose between three different upwinding schemes. This is done by setting the parameter ehfinder::upwind_type to either intrinsic, shift or characteristic.

The intrinsic scheme, looks at the values of \(f\) itself, to determine the direction of the stencil. This is basically in order to be able to handle situations like the one illustrated in 1D in Figure 2.

PIC


Figure 2: An illustration of how to choose the upwinding stencil when \(f\) is not differntiable everywhere

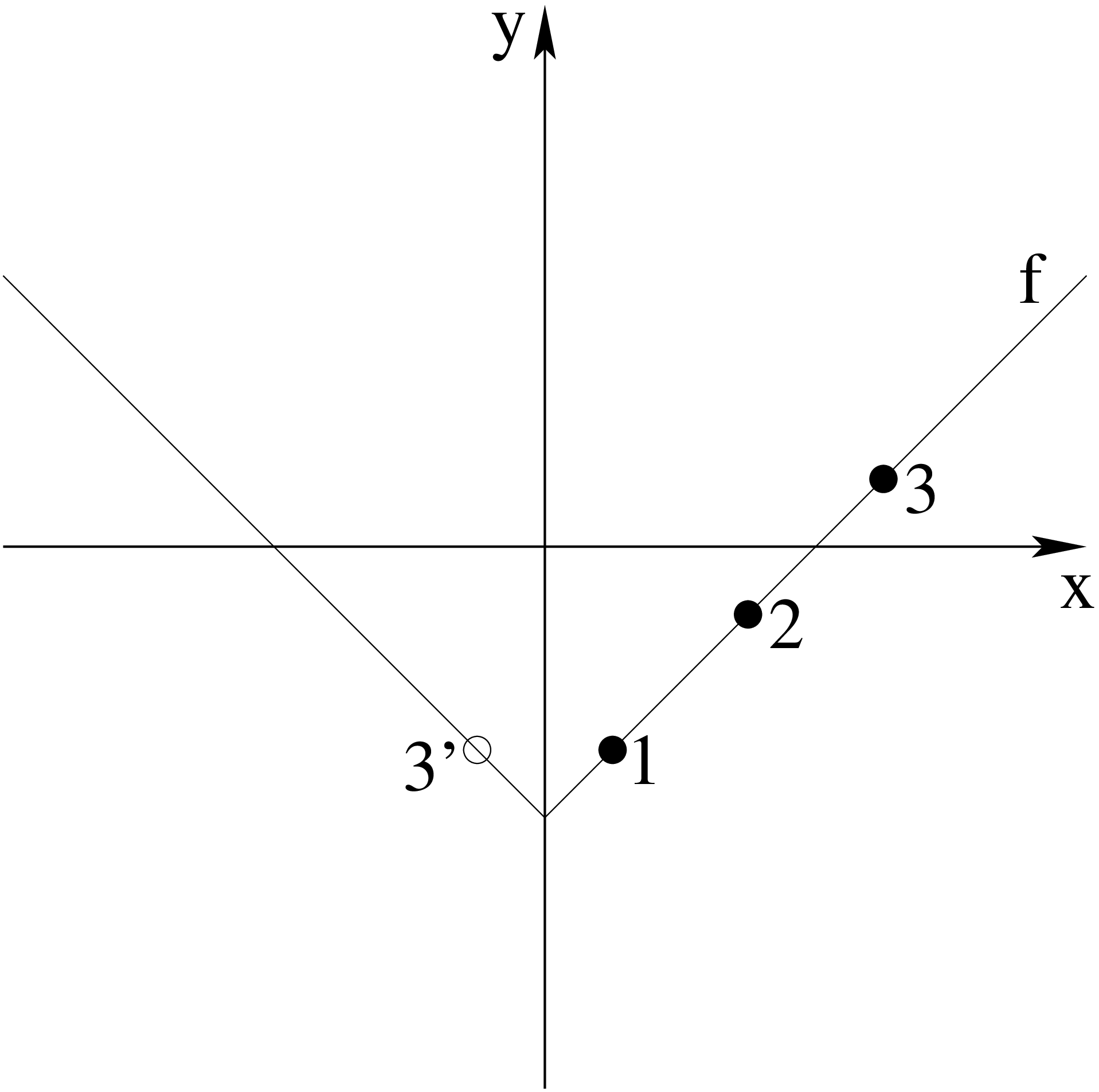
If the stencil for calculating derivatives in the point labeled 1 is taken to consist of the points 1, 2 and 3’, the non differentiablility of \(f\) may cause problems. The algorithm detects this and instead uses the points 1, 2, 3 as the stencil. This ensures that a non differentiable feature can be maintained in the evolution.

However this scheme only works in a few simple cases. For more general cases it is important to use characteristic information in order to ensure that the numerical stencil contains the domain of dependence. Therefore the characteristic scheme was introduced. Fortunately, by using the information contained in the level set functions the characteristic of the level set function can be calculated using \begin {equation} \frac {dx^{i}}{dt}=-\beta ^{i}+\frac {\alpha ^{2}\gamma ^{ij}\partial _{j}f} {\sqrt {\alpha ^{2}\gamma ^{kl}\partial _{k}f\partial _{l}f}}. \label {eq:char} \end {equation} The method estimates the characteristic direction using centered finite differences in equation (??) and then recalculates the one sided finite differences in the appropriate direction.

It might happen that the upwinding direction based on the characteristic direction results in the stencil to consist of the points 1, 2, 3’ in Figure 2. However, if the re-initialization is done often enough, this turns out not to cause any problems.

The shift scheme was implemented as an improvement to the intrinsic scheme but it turned out that the characteristic scheme was superior. Therefore shift upwinding should not be used. It might be completely removed in future revisions.

For the re-initialization the default is to use the intrinsic second order scheme (the re-initialization doesn’t depend on where the surface is moving), so characteristic upwinding is not applicable. It is possible to use a first order intrinsic scheme, but this is, in my experience, not accurate enough. A centered differencing scheme is also available, but is only there for testing purposes and should never be used. These alternative schemes will probably be removed in the future.

6 The most important parameters

Here the most important parameters are described.

EHFinder also extends the following parameter from admbase in order to be able to read in initial data.

7 How to use EHFinder with numerical data

In this section I will try to describe in little more detail how EHFinder can be used to find the EH in a numerical spacetime.

7.1 Outputting numerical data

The first thing to make sure, is that enough data is output during the numerical run, to be able to reconstruct the full 4-metric. The required output therefore consists of the ADMBase::metric, ADMBase::lapse and ADMBase::shift. However if the evolution was done with zero shift and/or lapse equal to one, it is not necessary to output these grid functions, as long as storage is turned on and they are set to the correct value initially when EHFinder is run. If the evolution was done with a conformal factor then StaticConformal::psi has to be output as well, since it is necessary in order to reconstruct the 4-metric. However it is only necessary to output this once since it is constant during the evolution. It is not necessary to output the derivatives of the conformal factor. If excision was used in the numerical run then it is also necessary to output SpaceMask::emask1 , since EHFinder has to make sure that its internal mask covers the space mask.

At present it is necessary to output all timesteps into the same file (use IO::out_timesteps_per_file = -1, which is the default). In principle both FLEXIO and HDF5 output should be supported, but only HDF5 output has been tested. Since EHFinder can be run on a lot less processors compared to the spacetime evolution, it is often advantageous to either do unchuncked output or to recombine the output files, since it is then possible to read the data onto a smaller number of processors (use IO::out_unchunked = "yes" to write unchunked data). If the numerical run is larger than the EH containing region (hopefully that is the case; otherwise the boundaries are definitely to close in), it is possible to use hyperslabbing to just output the EH containing region (see for example CactusPUGHIO/IOHDF5 for details on this). If hyperslabbing is used it is definitely necessary to do the output unchunked or recombine afterwards. An example parameter file can be seen in the par/Misner_2.2_80_3D.par.

In principle EHFinder should also work for downsampled (in both space and time) data, but no experiments have been done so far to estimate the loss of accuracy (I have always used the full resolution and done output at every timestep).

If hyperslabbing and/or downsampling is used, it is the users responsibility (by specifying the right parameters in the parameter file) to ensure that EHFinder is run with the correct grid spacing and time step.

7.2 Tips for parameter choices

EHFinder is still under development and testing and can as yet not be used as a black box. But still I can give some guidelines and advice on how to proceed.

The first concern is to setup the initial guess for the surface. Ideally one would like to use at least two different initial surfaces. One surface completely inside the EH and one surface completely outside the EH. In practice it is often a good idea to use more than two different initial surfaces, since then the initial surfaces closest to the EH can be identified. Using the feature of evolving multiple level set functions at a time, this can be done while reading in the numerical data only once. The easiest way to get an initial surface inside the EH, is to set up the initial guess to be completely inside the apparent horizon (AH). To get an initial guess that is outside of the EH is not as easy. One way is to choose a surface, that starts to contract everywhere when evolved according to equation (??). However this is not a guarantee, since the EH can be expanding in the numerical coordinates. This of course means that it is necessary to do it by trial and error. Set up some initial guess evolve it for a little while, look at 3D output to determine if the surface is contracting everywhere and change the initial surface if necessary.

Then comes the question of how often to do the re-initialization and how much to excise. These parameters depend on the numerical data. In principle, since the re-initialization can move the surface, one wants to do it as rarely as possible. On the other hand, re-initialization is necessary in order to keep the evolution nicely controlled (by avoiding large gradients), so a compromise has to be found. This might require some experimentation. Because movements of the surface during re-initialization, usually only occurs close to moments of topology change, it might be necessary to evolve all the way beyond the change of topology and look at 3D output to see if any problems occured. If significant movement of the surface during re-initialization near the change of topology is observed, then try again with re-initialization undo activated. How often to do the re-initialization also depends on the width of the active region. If the active region around the surface is narrow, it might be necessary to re-initialize more often, since in this case the boundaries of the active region is closer to the surface. At the boundaries the stencil direction is dictated by the geometry and not \(f\) itself or the characteristics, which might cause instabilities if it is not re-initialized. Good values guesses for ehfinder::reinitialize_every_pde seems to in the range 5–10 at low or medium resolutions but can usually be increased for higher resolutions. For ehfinder::shell_width I normally use at least 7.

EHFinder does not yet work fully with the fixed mesh refinement driver Carpet, but this is under development. Currently the evolution of the level set function and the re-initialization works, but only with no inner and outer excision. The analysis routines to find areas of the surfaces does not work with Carpet. Reading in metric data has not been tested with Carpet.

This documentation will be updated, as input comes in from users.

Happy event horizon finding.

References

[1]   Diener P., 2003, 2003, Classical and Quantum Gravity, 20, 4901–4917, A New General Purpose Event Horizon Finder for 3D Numerical Spacetimes, gr-qc/0305039

8 Parameters

area_calculation_method
 Scope: private KEYWORD
Description: How should the areas be calculated
Range Default: standard
standard
Using a angular coordinate system on the surface
isosurface
Using an isosurface triangulation

area_interpolation_order
 Scope: private INT
Description: What order should be used for the area interpoation
Range Default: 3
1:*
A valid positive interpolation order

area_interpolator
 Scope: private STRING
Description: What interpolator should be used for the area
Range Default: Lagrange polynomial interpolation
.+
A valid interpolator name

cas_a
 Scope: private REAL
Description: Initial a coefficient of ovaloid of cassini
Range Default: 2.0
:
Any number (negative and positive are equivalent)

cas_b
 Scope: private REAL
Description: Initial b coefficient of ovaloid of cassini
Range Default: 2.05
:
Any number (negative and positive are equivalent)

center_x
 Scope: private REAL
Description: The x-coordinate of the center
Range Default: 0.0
*:*
Anything

center_y
 Scope: private REAL
Description: The y-coordinate of the center
Range Default: 0.0
*:*
Anything

center_z
 Scope: private REAL
Description: The z-coordinate of the center
Range Default: 0.0
*:*
Anything

cheat
 Scope: private BOOLEAN
Description: Should we cheat and evolve using the last data set for a while?
Default: no

cheat_iterations
 Scope: private INT
Description: For how many iterations should we cheat
Range Default: (none)
0:*
If you really want to cheat this should be positive

eh_lapse_type
 Scope: private KEYWORD
Description: Do we use numerical or analytic metric information
Range Default: numerical
numerical
Read in metric from numerical data
analytic
Use external analytic metric

eh_metric_type
 Scope: private KEYWORD
Description: Do we use numerical or analytic metric information
Range Default: numerical
numerical
Read in metric from numerical data
analytic
Use external analytic metric

eh_number_level_sets
 Scope: private INT
Description: How many level set functions should we evolve
Range Default: 1
1:10
Between 1 and 10

eh_shift_type
 Scope: private KEYWORD
Description: Do we use numerical or analytic metric information
Range Default: numerical
numerical
Read in metric from numerical data
analytic
Use external analytic metric

evolve_generators
 Scope: private BOOLEAN
Description: Should the generators be evolved
Default: no

file_type
 Scope: private KEYWORD
Description: Are the timesteps in separate files or in one file?
Range Default: one_file
one_file
All timesteps are in the same file
sep_time_files
Timesteps are in separete files

generator_distribution
 Scope: private KEYWORD
Description: What initial distribution should be used
Range Default: line
line
Put the generators on a line in the xz-plane
2D array
Put the generators on a surface with spherical topology

generator_interpolation_order
 Scope: private INT
Description: What order should be used for the generator interpoation
Range Default: 3
1:*
A valid positive interpolation order

generator_interpolator
 Scope: private STRING
Description: What interpolator should be used for the generators
Range Default: Lagrange polynomial interpolation
.+
A valid interpolator name

generator_tracking_method
 Scope: private KEYWORD
Description: What method should be used for tracking the generators
Range Default: interpolate_before
interpolate_before
Interpolate first, then calculate
interpolate_after
Calculate first, then interpolate

initial_a
 Scope: private REAL
Description: Initial a coefficient of ellipsoid
Range Default: 1.0
0.0:
Positive please

initial_b
 Scope: private REAL
Description: Initial b coefficient of ellipsoid
Range Default: 1.0
0.0:
Positive please

initial_c
 Scope: private REAL
Description: Initial c coefficient of ellipsoid
Range Default: 1.0
0.0:
Positive please

initial_f
 Scope: private KEYWORD
Description: Initial surface choice
Range Default: sphere
sphere
spherical surface
ellipsoid
ellipsoidal surface
cassini
ovaloid of cassini

initial_rad
 Scope: private REAL
Description: Initial radius of surface
Range Default: 1.0
0.0:
Positive please

last_iteration_number
 Scope: private INT
Description: The starting iteration number for the EH_Finder (last iteration number of the simulation)
Range Default: (none)
0:
Positive please

maximum_surface_number
 Scope: private INT
Description: The maximum number of surfaces expected in the data
Range Default: 1
1:*
Positive please

mode
 Scope: private KEYWORD
Description: Mode of operation
Range Default: normal
normal
Find event horizons
analysis
Provide storage for f without evolving
generator
Provide storage for f and initialize without evolving

n_array_ghosts
 Scope: private INT
Description: Number of ghost points in the surface grid array
Range Default: 1
1:
Positive please

nphi
 Scope: private INT
Description: Number of points in the phi direction when finding points on the surface
Range Default: 51
1:*:2
Positive and odd please

ntheta
 Scope: private INT
Description: Number of points in the theta direction when finding points on the surface
Range Default: 51
1:*:2
Positive and odd please

number_of_generators
 Scope: private INT
Description: How many generators should be evolved
Range Default: 1
1:*
Postive please

number_of_generators_phi
 Scope: private INT
Description: How many generators in the phi direction
Range Default: 1
1:*
Positive please

number_of_generators_theta
 Scope: private INT
Description: How many generators in the theta direction
Range Default: 1
1:*
Positive please

pde_differences
 Scope: private KEYWORD
Description: Type of finite diffencing used in pde re-initialization
Range Default: upwind2
centered
Use 2nd order centered differences except at the boundaries
upwind
Use 1st order upwinded differences everywhere
upwind2
Use 2nd order upwinded differences everywhere

re_init_int_method
 Scope: private KEYWORD
Description: Integration method used in re-initialization
Range Default: euler
euler
Standard euler scheme
rk2
Second order Runge-Kutta scheme

re_init_max_iter
 Scope: private INT
Description: maximum number of iterations in the re-initialization
Range Default: 800
0:
Positive please

re_init_undo
 Scope: private BOOLEAN
Description: Should re-initialization be undone at pinch-off
Default: yes

re_init_verbose
 Scope: private BOOLEAN
Description: Should re-initialization be verbose?
Default: no

re_initialize_every
 Scope: private INT
Description: How often to re-initialize the level set function
Range Default: 10
0:
If 0 don’t re-initialize

read_conformal_factor_once
 Scope: private BOOLEAN
Description: Should the conformal factor only be read once
Default: yes

rotation_alpha
 Scope: private REAL
Description: Rotation angle around z-axis of ellipsoid
Range Default: 0.0
*:*
Everything is possible

rotation_beta
 Scope: private REAL
Description: Rotation angle around y-axis of ellipsoid
Range Default: 0.0
*:*
Everything is possible

rotation_gamma
 Scope: private REAL
Description: Rotation angle around x-axis of ellipsoid
Range Default: 0.0
*:*
Everything is possible

saved_iteration_every
 Scope: private INT
Description: How often was the numerical data saved
Range Default: 1
1:
Positive please

shell_width
 Scope: private REAL
Description: Width of the evolution region in units of the grid spacing
Range Default: 7.0
0.0:
Positive please

surface_direction
 Scope: private KEYWORD
Description: Should we track outward or inward moving surfaces
Range Default: outward
outward
Track outward moving surfaces. Use for event horizon finding.
inward
Track inward moving surfaces.

surface_interpolation_order
 Scope: private INT
Description: What order should be used for the surface interpoation
Range Default: 2
1:*
A valid positive interpolation order

surface_interpolator
 Scope: private STRING
Description: What interpolator should be used to locate the surface
Range Default: Hermite polynomial interpolation
.+
A valid interpolator name

translate_x
 Scope: private REAL
Description: Translation in x-direction
Range Default: 0.0
*:*
Everything is possible

translate_y
 Scope: private REAL
Description: Translation in y-direction
Range Default: 0.0
*:*
Everything is possible

translate_z
 Scope: private REAL
Description: Translation in z-direction
Range Default: 0.0
*:*
Everything is possible

upwind_type
 Scope: private KEYWORD
Description: Type of upwinding used in evolving the ehfinder equations
Range Default: characteristic
intrinsic
Use the values of f itself to determine upwind direction
shift
Use the shift to determine upwind direction
characteristic
Use characteristic information

use_inner_excision
 Scope: private BOOLEAN
Description: Should inner excision be used?
Default: yes

use_outer_excision
 Scope: private BOOLEAN
Description: Should outer excision be used?
Default: yes

use_user_center
 Scope: private BOOLEAN
Description: Should the user prescribed center be used
Default: no

ehfinder_max_evolved_array_size
Scope: restricted INT
Description: The maximum size of evolved grid arrays used by EHFinder
Range Default: 1
1:*
The size of the generator grid arrays

ehfinder_maxnumevolvedvars
 Scope: restricted INT
Description: The maximum number of evolved variables used by EHFinder
Range Default: 1
1:10
Only evolve the level set functions

ehfinder_num_arrayevolved_vars
 Scope: restricted INT
Description: The maximum number of evolved grid arrays used by EHFinder
Range Default: 3
0:30
Should be exactly zero or a multiple of three

use_mask
 Scope: shared from SPACEMASKBOOLEAN

9 Interfaces

General

Implements:

ehfinder

Inherits:

grid

admbase

coordgauge

staticconformal

spacemask

boundary

Grid Variables

9.0.1 PRIVATE GROUPS

  Group Names     Variable Names   Details    
f f compact 0
dimensions 3
distribution DEFAULT
group type GF
timelevels 3
vararray_size eh_number_level_sets
variable type REAL
sf sf compact 0
dimensions 3
distribution DEFAULT
group type GF
tags tensortypealias=”Scalar” Prolongation=”None”
timelevels 1
vararray_size eh_number_level_sets
variable type REAL
dfx dfx compact 0
dimensions 3
distribution DEFAULT
group type GF
tags Prolongation=”None”
timelevels 1
vararray_size eh_number_level_sets
variable type REAL
dfy dfy compact 0
dimensions 3
distribution DEFAULT
group type GF
tags Prolongation=”None”
timelevels 1
vararray_size eh_number_level_sets
variable type REAL
dfz dfz compact 0
dimensions 3
distribution DEFAULT
group type GF
tags Prolongation=”None”
timelevels 1
vararray_size eh_number_level_sets
variable type REAL
dfsq dfsq compact 0
dimensions 3
distribution DEFAULT
group type GF
tags tensortypealias=”Scalar” Prolongation=”None”
timelevels 1
vararray_size eh_number_level_sets
variable type REAL

  Group Names     Variable Names   Details    
ftmp ftmp compact 0
dimensions 3
distribution DEFAULT
group type GF
tags tensortypealias=”Scalar” Prolongation=”None”
timelevels 1
vararray_size eh_number_level_sets
variable type REAL
sftmp sftmp compact 0
dimensions 3
distribution DEFAULT
group type GF
tags tensortypealias=”Scalar” Prolongation=”None”
timelevels 1
vararray_size eh_number_level_sets
variable type REAL
fbak fbak compact 0
dimensions 3
distribution DEFAULT
group type GF
tags tensortypealias=”Scalar” Prolongation=”None”
timelevels 1
vararray_size eh_number_level_sets
variable type REAL
g3inv compact 0
g3xx description The inverse of the 3-metric
g3xy dimensions 3
g3xz distribution DEFAULT
g3yy group type GF
g3yz tags tensortypealias=”Scalar” Prolongation=”None”
g3zz timelevels 1
variable type REAL
eh_mask eh_mask compact 0
dimensions 3
distribution DEFAULT
group type GF
tags tensortypealias=”Scalar” Prolongation=”None”
timelevels 1
vararray_size eh_number_level_sets
variable type INT
tm_mask tm_mask compact 0
dimensions 3
distribution DEFAULT
group type GF
tags tensortypealias=”Scalar” Prolongation=”None”
timelevels 1
vararray_size eh_number_level_sets
variable type INT

  Group Names     Variable Names   Details    
eh_mask_bak eh_mask_bak compact 0
dimensions 3
distribution DEFAULT
group type GF
tags tensortypealias=”Scalar” Prolongation=”None”
timelevels 1
vararray_size eh_number_level_sets
variable type INT
re_init_control re_init_control compact 0
dimensions 0
distribution CONSTANT
group type SCALAR
timelevels 1
variable type INT
niter_reinit niter_reinit compact 0
dimensions 0
distribution CONSTANT
group type SCALAR
timelevels 1
variable type INT
surface_index compact 0
sc dimensions 3
distribution DEFAULT
group type GF
tags tensortypealias=”Scalar” Prolongation=”None”
timelevels 1
variable type REAL
find_surface_status find_surface_status compact 0
dimensions 0
distribution CONSTANT
group type SCALAR
timelevels 1
variable type INT
levelset_integers compact 0
levelset_counter description Integer variables used to loop over the level sets
more_levelsets dimensions 0
distribution CONSTANT
group type SCALAR
timelevels 1
variable type INT

  Group Names     Variable Names   Details    
surface_integers compact 0
surface_counter description Integer variables used in surface integration
points_counter dimensions 0
more_surfaces distribution CONSTANT
more_points group type SCALAR
integrate_counter timelevels 1
variable type INT
surface_reals compact 0
sym_factor description Real variables used in surface integration
theta_sym_factor dimensions 0
phi_sym_factor distribution CONSTANT
group type SCALAR
timelevels 1
variable type REAL
surface_arrays compact 0
ctheta description Grid arrays for points on the surface
cphi dimensions 2
rsurf distribution DEFAULT
sintheta ghostsize N_ARRAY_GHOSTS
  ghostsize N_ARRAY_GHOSTS
costheta group type ARRAY
sinphi size NTHETA
  size NPHI
cosphi timelevels 1
drdtheta variable type REAL
surface_tmp_arrays compact 0
drsurf description Temporary grid arrays for finding points on the surface
interp_x dimensions 2
interp_y distribution DEFAULT
interp_z ghostsize N_ARRAY_GHOSTS
  ghostsize N_ARRAY_GHOSTS
f_interp group type ARRAY
dfdx_interp size NTHETA
  size NPHI
dfdy_interp timelevels 1
dfdz_interp variable type REAL
center_arrays compact 0
center description The cartesian location of the center for the spherical coordinate system
dimensions 1
distribution CONSTANT
group type ARRAY
size 3
timelevels 1
variable type REAL
surface_int_array compact 0
n_since_last_reduction description Temporary integer grid array for finding points on the surface
dimensions 2
distribution DEFAULT
ghostsize N_ARRAY_GHOSTS
  ghostsize N_ARRAY_GHOSTS
group type ARRAY
size NTHETA
  size NPHI
timelevels 1
variable type INT

  Group Names     Variable Names   Details    
interp_metric_arrays compact 0
gxxi description Arrays for holding the interpolated metric and conformal factor
gxyi dimensions 2
gxzi distribution DEFAULT
gyyi ghostsize N_ARRAY_GHOSTS
  ghostsize N_ARRAY_GHOSTS
gyzi group type ARRAY
gzzi size NTHETA
  size NPHI
psii timelevels 1
variable type REAL
integrate_tmp_array compact 0
int_tmp description Temporary array that is used in the integration of various quantities
dimensions 2
distribution DEFAULT
ghostsize N_ARRAY_GHOSTS
  ghostsize N_ARRAY_GHOSTS
group type ARRAY
size NTHETA
  size NPHI
timelevels 1
variable type REAL
eh_area eh_area compact 0
dimensions 1
distribution DEFAULT
ghostsize 0
group type ARRAY
size MAXIMUM_SURFACE_NUMBER
timelevels 1
vararray_size eh_number_level_sets
variable type REAL
eh_area2 eh_area2 compact 0
dimensions 1
distribution DEFAULT
ghostsize 0
group type ARRAY
size MAXIMUM_SURFACE_NUMBER
timelevels 1
vararray_size eh_number_level_sets
variable type REAL
eh_centroid_x eh_centroid_x compact 0
dimensions 1
distribution DEFAULT
ghostsize 0
group type ARRAY
size MAXIMUM_SURFACE_NUMBER
timelevels 1
vararray_size eh_number_level_sets
variable type REAL
eh_centroid_y eh_centroid_y compact 0
dimensions 1
distribution DEFAULT
ghostsize 0
group type ARRAY
size MAXIMUM_SURFACE_NUMBER
timelevels 1
vararray_size eh_number_level_sets
variable type REAL

  Group Names     Variable Names   Details    
eh_centroid_z eh_centroid_z compact 0
dimensions 1
distribution DEFAULT
ghostsize 0
group type ARRAY
size MAXIMUM_SURFACE_NUMBER
timelevels 1
vararray_size eh_number_level_sets
variable type REAL
eh_centroid2_x eh_centroid2_x compact 0
dimensions 1
distribution DEFAULT
ghostsize 0
group type ARRAY
size MAXIMUM_SURFACE_NUMBER
timelevels 1
vararray_size eh_number_level_sets
variable type REAL
eh_centroid2_y eh_centroid2_y compact 0
dimensions 1
distribution DEFAULT
ghostsize 0
group type ARRAY
size MAXIMUM_SURFACE_NUMBER
timelevels 1
vararray_size eh_number_level_sets
variable type REAL
eh_centroid2_z eh_centroid2_z compact 0
dimensions 1
distribution DEFAULT
ghostsize 0
group type ARRAY
size MAXIMUM_SURFACE_NUMBER
timelevels 1
vararray_size eh_number_level_sets
variable type REAL
eh_circ_eq eh_circ_eq compact 0
dimensions 1
distribution DEFAULT
ghostsize 0
group type ARRAY
size MAXIMUM_SURFACE_NUMBER
timelevels 1
vararray_size eh_number_level_sets
variable type REAL
eh_circ_pol eh_circ_pol compact 0
dimensions 1
distribution DEFAULT
ghostsize 0
group type ARRAY
size MAXIMUM_SURFACE_NUMBER
timelevels 1
vararray_size eh_number_level_sets
variable type REAL

  Group Names     Variable Names   Details    
eh_circ_eq2 eh_circ_eq2 compact 0
dimensions 1
distribution DEFAULT
ghostsize 0
group type ARRAY
size MAXIMUM_SURFACE_NUMBER
timelevels 1
vararray_size eh_number_level_sets
variable type REAL
eh_circ_pol2 eh_circ_pol2 compact 0
dimensions 1
distribution DEFAULT
ghostsize 0
group type ARRAY
size MAXIMUM_SURFACE_NUMBER
timelevels 1
vararray_size eh_number_level_sets
variable type REAL
xg xg compact 0
dimensions 1
distribution DEFAULT
ghostsize 0
group type ARRAY
size NUMBER_OF_GENERATORS
timelevels 3
vararray_size eh_number_level_sets
variable type REAL
yg yg compact 0
dimensions 1
distribution DEFAULT
ghostsize 0
group type ARRAY
size NUMBER_OF_GENERATORS
timelevels 3
vararray_size eh_number_level_sets
variable type REAL
zg zg compact 0
dimensions 1
distribution DEFAULT
ghostsize 0
group type ARRAY
size NUMBER_OF_GENERATORS
timelevels 3
vararray_size eh_number_level_sets
variable type REAL
dxg dxg compact 0
dimensions 1
distribution DEFAULT
ghostsize 0
group type ARRAY
size NUMBER_OF_GENERATORS
timelevels 1
vararray_size eh_number_level_sets
variable type REAL

  Group Names     Variable Names   Details    
dyg dyg compact 0
dimensions 1
distribution DEFAULT
ghostsize 0
group type ARRAY
size NUMBER_OF_GENERATORS
timelevels 1
vararray_size eh_number_level_sets
variable type REAL
dzg dzg compact 0
dimensions 1
distribution DEFAULT
ghostsize 0
group type ARRAY
size NUMBER_OF_GENERATORS
timelevels 1
vararray_size eh_number_level_sets
variable type REAL
generator_arrays compact 0
alpg description Arrays to hold the interpolated metric
  description gauge and level set data
betaxg dimensions 1
betayg distribution DEFAULT
betazg ghostsize 0
gxxg group type ARRAY
gxyg size NUMBER_OF_GENERATORS
gxzg timelevels 1
gyyg variable type REAL
generator_gf compact 0
xgf description Temporary grid function used in calculating the right hand side of the generator evolution equation
ygf dimensions 3
zgf distribution DEFAULT
group type GF
tags Prolongation=”None”
timelevels 1
variable type REAL
xg2 xg2 compact 0
dimensions 2
distribution DEFAULT
ghostsize 0
  ghostsize 0
group type ARRAY
size NUMBER_OF_GENERATORS_THETA
  size NUMBER_OF_GENERATORS_PHI
timelevels 3
vararray_size eh_number_level_sets
variable type REAL
yg2 yg2 compact 0
dimensions 2
distribution DEFAULT
ghostsize 0
  ghostsize 0
group type ARRAY
size NUMBER_OF_GENERATORS_THETA
  size NUMBER_OF_GENERATORS_PHI
timelevels 3
vararray_size eh_number_level_sets
variable type REAL

  Group Names     Variable Names   Details    
zg2 zg2 compact 0
dimensions 2
distribution DEFAULT
ghostsize 0
  ghostsize 0
group type ARRAY
size NUMBER_OF_GENERATORS_THETA
  size NUMBER_OF_GENERATORS_PHI
timelevels 3
vararray_size eh_number_level_sets
variable type REAL
dxg2 dxg2 compact 0
dimensions 2
distribution DEFAULT
ghostsize 0
  ghostsize 0
group type ARRAY
size NUMBER_OF_GENERATORS_THETA
  size NUMBER_OF_GENERATORS_PHI
timelevels 1
vararray_size eh_number_level_sets
variable type REAL
dyg2 dyg2 compact 0
dimensions 2
distribution DEFAULT
ghostsize 0
  ghostsize 0
group type ARRAY
size NUMBER_OF_GENERATORS_THETA
  size NUMBER_OF_GENERATORS_PHI
timelevels 1
vararray_size eh_number_level_sets
variable type REAL
dzg2 dzg2 compact 0
dimensions 2
distribution DEFAULT
ghostsize 0
  ghostsize 0
group type ARRAY
size NUMBER_OF_GENERATORS_THETA
  size NUMBER_OF_GENERATORS_PHI
timelevels 1
vararray_size eh_number_level_sets
variable type REAL
generator_arrays2 compact 0
alpg2 description Arrays to hold the interpolated metric
  description gauge and level set data
betaxg2 dimensions 2
betayg2 distribution DEFAULT
betazg2 ghostsize 0
  ghostsize 0
gxxg2 group type ARRAY
gxyg2 size NUMBER_OF_GENERATORS_THETA
  size NUMBER_OF_GENERATORS_PHI
gxzg2 timelevels 1
gyyg2 variable type REAL
generator_gf2 compact 0
xgf2 description Temporary grid function used in calculating the right hand side of the generator evolution equation
ygf2 dimensions 3
zgf2 distribution DEFAULT
group type GF
tags Prolongation=”None”
timelevels 1
variable type REAL

Uses header:

Boundary.h

carpet.h

10 Schedule

This section lists all the variables which are assigned storage by thorn EinsteinAnalysis/EHFinder. Storage can either last for the duration of the run (Always means that if this thorn is activated storage will be assigned, Conditional means that if this thorn is activated storage will be assigned for the duration of the run if some condition is met), or can be turned on for the duration of a schedule function.

Storage

 

  Conditional:
  f[1]
  f[2]
  levelset_integers
  center_arrays
  xg[2] yg[2] zg[2]
  dxg dyg dzg
  xg2[2] yg2[2] zg2[2]
  dxg2 dyg2 dzg2
  sf
  ftmp
  sftmp
  eh_mask
  surface_arrays
  eh_area2 eh_centroid2_x eh_centroid2_y eh_centroid2_z
  eh_circ_eq2 eh_circ_pol2
  find_surface_status
   

Scheduled Functions

CCTK_PARAMCHECK (conditional)

  ehfinder_paramcheck

  check parameters

 

  Language: fortran
  Type: function

CCTK_INITIAL (conditional)

  ehfinder_read_metric

  read in metric from file

 

  Language: fortran
  Type: function

CCTK_POST_RECOVER_VARIABLES (conditional)

  ehfinder_initweights

  setup weights for simpson integration

 

  Language: fortran
  Type: function

CCTK_ANALYSIS (conditional)

  ehfinder_level_sets

  loop over the level set functions

 

  Triggers: eh_area
    eh_centroid_x
    eh_centroid_y
    eh_centroid_z
    eh_circ_eq
    eh_circ_pol
  Type: group

EHFinder_Level_Sets (conditional)

  ehfinder_levelsetloopinit

  initialize the loop counter over the level set functions

 

  Language: fortran
  Triggers: eh_area
    eh_centroid_x
    eh_centroid_y
    eh_centroid_z
    eh_circ_eq
    eh_circ_pol
  Type: function

EHFinder_Level_Sets (conditional)

  ehfinder_surfaces

  count the number of surfaces and integrate over them

 

  Storage: surface_integers
    surface_reals
    surface_index
  Triggers: eh_area
    eh_centroid_x
    eh_centroid_y
    eh_centroid_z
    eh_circ_eq
    eh_circ_pol
  Type: group
  While: ehfinder::more_levelsets

EHFinder_Surfaces (conditional)

  ehfinder_countsurfacesinit

  initialize while loop control

 

  Language: fortran
  Triggers: eh_area
    eh_centroid_x
    eh_centroid_y
    eh_centroid_z
    eh_circ_eq
    eh_circ_pol
  Type: function

EHFinder_Surfaces (conditional)

  ehfinder_countmarksurfaces

  counting and mark surfaces

 

  After: ehfinder_countsurfacesinit
  Triggers: eh_area
    eh_centroid_x
    eh_centroid_y
    eh_centroid_z
    eh_circ_eq
    eh_circ_pol
  Type: group
  While: ehfinder::more_surfaces

EHFinder_CountMarkSurfaces (conditional)

  ehfinder_countsurfaces

  check if there are more surfaces

 

  Language: fortran
  Sync: surface_index
  Triggers: eh_area
    eh_centroid_x
    eh_centroid_y
    eh_centroid_z
    eh_circ_eq
    eh_circ_pol
  Type: function

EHFinder_CountMarkSurfaces (conditional)

  ehfinder_markpoints

  marking surfaces

 

  After: ehfinder_countsurfaces
  Triggers: eh_area
    eh_centroid_x
    eh_centroid_y
    eh_centroid_z
    eh_circ_eq
    eh_circ_pol
  Type: group
  While: ehfinder::more_points

EHFinder_MarkPoints (conditional)

  ehfinder_marksurfaces

  mark points inside the current surface

 

  Language: fortran
  Sync: surface_index
  Triggers: eh_area
    eh_centroid_x
    eh_centroid_y
    eh_centroid_z
    eh_circ_eq
    eh_circ_pol
  Type: function

EHFinder_MarkPoints (conditional)

  ehfinder_applysymsc

  select the surface counter grid function for boundary conditions

 

  After: ehfinder_marksurfaces
  Language: fortran
  Triggers: eh_area
    eh_centroid_x
    eh_centroid_y
    eh_centroid_z
    eh_circ_eq
    eh_circ_pol
  Type: function

CCTK_INITIAL (conditional)

  ehfinder_read_lapse

  read in lapse from file

 

  Language: fortran
  Type: function

EHFinder_MarkPoints (conditional)

  applybcs

  apply boundary conditions (symmetries)

 

  After: ehfinder_applysymsc
  Type: group

EHFinder_Surfaces (conditional)

  ehfinder_infosurfaces

  output info about found surfaces

 

  After: ehfinder_countmarksurfaces
  Language: fortran
  Triggers: eh_area
    eh_centroid_x
    eh_centroid_y
    eh_centroid_z
    eh_circ_eq
    eh_circ_pol
  Type: function

EHFinder_Surfaces (conditional)

  ehfinder_integration

  find and integrate over surfaces

 

  After: ehfinder_infosurfaces
  Triggers: eh_area
    eh_centroid_x
    eh_centroid_y
    eh_centroid_z
    eh_circ_eq
    eh_circ_pol
  Type: group
  While: ehfinder::integrate_counter

EHFinder_Integration (conditional)

  ehfinder_findsurface

  find surface

 

  Language: fortran
  Storage: surface_tmp_arrays
    surface_int_array
  Sync: surface_arrays
  Triggers: eh_area
    eh_centroid_x
    eh_centroid_y
    eh_centroid_z
    eh_circ_eq
    eh_circ_pol
  Type: function

EHFinder_Integration (conditional)

  ehfinder_findsurfaceelement

  find surface area element

 

  After: ehfinder_findsurface
  Language: fortran
  Storage: surface_tmp_arrays
    interp_metric_arrays
  Triggers: eh_area
    eh_centroid_x
    eh_centroid_y
    eh_centroid_z
    eh_circ_eq
    eh_circ_pol
  Type: function

EHFinder_Integration (conditional)

  ehfinder_integratearea

  calculate area integrals

 

  After: ehfinder_findsurfaceelement
  Language: fortran
  Storage: integrate_tmp_array
  Triggers: eh_area
    eh_centroid_x
    eh_centroid_y
    eh_centroid_z
    eh_circ_eq
    eh_circ_pol
  Type: function

EHFinder_Integration (conditional)

  ehfinder_integratecentroid

  calculate centroid integrals

 

  After: ehfinder_integratearea
  Language: fortran
  Storage: surface_tmp_arrays
    integrate_tmp_array
  Triggers: eh_centroid_x
    eh_centroid_y
    eh_centroid_z
  Type: function

EHFinder_Integration (conditional)

  ehfinder_integratecircumference

  calculate circumferences

 

  After: ehfinder_integratearea
  Language: fortran
  Storage: surface_tmp_arrays
    integrate_tmp_array
  Triggers: eh_circ_eq
    eh_circ_pol
  Type: function

EHFinder_Surfaces (conditional)

  ehfinder_updatecounter

  update the loop variables

 

  Language: fortran
  Triggers: eh_area
    eh_centroid_x
    eh_centroid_y
    eh_centroid_z
    eh_circ_eq
    eh_circ_pol
  Type: function

CCTK_ANALYSIS (conditional)

  ehfinder_copyarea

  copy areas to output variable

 

  After: ehfinder_level_sets
  Language: fortran
  Storage: eh_area
  Triggers: eh_area
  Type: function

CCTK_INITIAL (conditional)

  ehfinder_read_shift

  read in shift from file

 

  Language: fortran
  Type: function

CCTK_ANALYSIS (conditional)

  ehfinder_copycentroid

  copy centroids to output variable

 

  After: ehfinder_level_sets
  Language: fortran
  Storage: eh_centroid_x
    eh_centroid_y
    eh_centroid_z
  Triggers: eh_centroid_x
    eh_centroid_y
    eh_centroid_z
  Type: function

CCTK_ANALYSIS (conditional)

  ehfinder_copycircumference

  copy circumferences to output variable

 

  After: ehfinder_level_sets
  Language: fortran
  Storage: eh_circ_eq
    eh_circ_pol
  Triggers: eh_circ_eq
    eh_circ_pol
  Type: function

CCTK_ANALYSIS (conditional)

  ehfinder_isosurfacearea

  find isosurfaces and calculate the area

 

  Triggers: eh_area
  Type: group

EHFinder_IsoSurfaceArea (conditional)

  ehfinder_isosurface

  find isosurfaces

 

  Language: fortran
  Storage: eh_area
  Triggers: eh_area
  Type: function

CCTK_PRESTEP (conditional)

  ehfinder_read_metric

  read in metric from file

 

  Language: fortran
  Type: function

CCTK_PRESTEP (conditional)

  ehfinder_read_lapse

  read in lapse from file

 

  Language: fortran
  Type: function

CCTK_PRESTEP (conditional)

  ehfinder_read_shift

  read in shift from file

 

  Language: fortran
  Type: function

CCTK_PRESTEP (conditional)

  ehfinder_read_conformal

  read in conformal factor from file

 

  Language: fortran
  Type: function

CCTK_PRESTEP (conditional)

  ehfinder_read_mask

  read in excision mask from file

 

  Language: fortran
  Type: function

MoL_Register (conditional)

  ehfinder_molregister

  register evolution variables

 

  Language: fortran
  Type: function

CCTK_INITIAL (conditional)

  ehfinder_read_conformal

  read in conformal factor from file

 

  Language: fortran
  Type: function

CCTK_BASEGRID (conditional)

  ehfinder_setsym

  register the symmetries for the level set function

 

  Language: fortran
  Storage: sftmp
  Type: function

CCTK_POSTINITIAL (conditional)

  ehfinder_maskinit

  setup the initial mask

 

  After: ehfinder_init
  Language: fortran
  Type: function

MoL_CalcRHS (conditional)

  ehfinder_sources

  calculate the source terms

 

  Language: fortran
  Storage: dfx
    dfy
    dfz
    g3inv
  Type: function

MoL_CalcRHS (conditional)

  ehfinder_generator_sources

  calculate the source terms for the generator evolution

 

  Language: fortran
  Storage: generator_arrays
  Type: function

MoL_CalcRHS (conditional)

  ehfinder_generator_sources_2d

  calculate the source terms for the 2d generator evolution

 

  Language: fortran
  Storage: generator_arrays2
  Type: function

MoL_CalcRHS (conditional)

  ehfinder_generator_sources2

  calculate the source terms2 for the generator evolution

 

  After: ehfinder_sources
  Language: fortran
  Storage: generator_arrays
  Type: function

MoL_PostStep (conditional)

  ehfinder_poststep

  schedule group for symmetry boundaries and syncing

 

  Type: group

EHFinder_PostStep (conditional)

  ehfinder_applysymf

  select f for boundary conditions

 

  Language: fortran
  Sync: f
    sftmp
  Type: function

EHFinder_PostStep (conditional)

  applybcs

  apply boundary conditions (symmetries)

 

  After: ehfinder_applysymf
  Type: group

CCTK_POSTSTEP (conditional)

  ehfinder_reinitialize

  re-initialize the level set function

 

  Storage: fbak
    eh_mask_bak
    re_init_control
    niter_reinit
  Type: group

CCTK_INITIAL (conditional)

  ehfinder_read_mask

  read in excision mask from file

 

  After: maskone
  Language: fortran
  Type: function

(conditional)

  ehfinder_prereinitialize

  routines for re-initialization control

 

  Type: group

EHFinder_PreReInitialize (conditional)

  ehfinder_reinitializecontrol

  initializes the re-initialization control

 

  Language: fortran
  Options: global
  Type: function

EHFinder_PreReInitialize (conditional)

  ehfinder_reinitializeinitialize

  initializes variables for reinitialization

 

  After: ehfinder_reinitializecontrol
  Language: fortran
  Type: function

(conditional)

  euler_reinitializeevolve

  schedule group for euler re-initialization evolution

 

  Type: group

Euler_ReInitializeEvolve (conditional)

  ehfinder_reinitializeeuler

  euler scheme

 

  Language: fortran
  Storage: dfx
    dfy
    dfz
    dfsq
  Type: function

Euler_ReInitializeEvolve (conditional)

  ehfinder_applysymfsftmp

  select f for boundary conditions

 

  After: ehfinder_reinitializeeuler
  Language: fortran
  Sync: f
    sftmp
  Type: function

Euler_ReInitializeEvolve (conditional)

  applybcs

  apply boundary conditions (symmetries)

 

  After: ehfinder_applysymf
  Type: group

(conditional)

  euler_poststep

  schedule group for euler re-initialization post step

 

  Type: group

Euler_PostStep (conditional)

  ehfinder_reinitializepoststep

  check if the re-initialization is done

 

  Language: fortran
  Options: global
  Type: function

EHFinder_ReInitialize (conditional)

  ehfinder_prereinitialize

  pugh version of the pre-re-initialization routines

 

  Type: group

CCTK_INITIAL (conditional)

  ehfinder_init

  setup local variables

 

  Language: fortran
  Sync: f
  Type: function

EHFinder_ReInitialize (conditional)

  euler_reinitialize

  schedule group for euler re-initialization

 

  After: ehfinder_prereinitializepugh
  Type: group
  While: ehfinder::re_init_control

Euler_ReInitialize (conditional)

  euler_reinitializeevolve

  schedule group for euler re-initialization evolution with pugh

 

  Type: group

Euler_ReInitialize (conditional)

  euler_poststep

  schedule group for euler re-initialization post step

 

  After: euler_reinitializeevolve
  Type: group

EHFinder_ReInitialize (conditional)

  ehfinder_reinitialize_check

  check to see if re-initialization has to be undone

 

  After: euler_reinitialize
  Language: fortran
  Type: function

EHFinder_ReInitialize (conditional)

  ehfinder_prereinitialize_carpet

  carpet version of the pre-reinitialization routines

 

  Language: c
  Options: level
  Type: function

EHFinder_ReInitialize (conditional)

  ehfinder_reinitialize_wrapper

  wrapper routine for euler re-initialization for carpet

 

  After: ehfinder_prereinitialize_carpet
  Language: c
  Options: level
  Type: function
  While: ehfinder::re_init_control

EHFinder_ReInitialize (conditional)

  rk2_reinitialize

  schedule group for rk2 re-initialization

 

  After: ehfinder_reinitializecontrol
  Type: group
  While: ehfinder::re_init_control

RK2_ReInitialize (conditional)

  ehfinder_reinitializerk2_1

  rk2 scheme step 1

 

  Language: fortran
  Storage: dfx
    dfy
    dfz
    dfsq
  Type: function

RK2_ReInitialize (conditional)

  ehfinder_applysymf

  select f for boundary conditions

 

  After: ehfinder_reinitializerk2_1
  Language: fortran
  Sync: f
  Type: function

RK2_ReInitialize (conditional)

  applybcs

  apply boundary conditions (symmetries)

 

  After: sym_rk2_1
  Type: group

CCTK_INITIAL (conditional)

  ehfinder_init_f

  setup the initial surface

 

  Language: fortran
  Sync: f
  Type: function

RK2_ReInitialize (conditional)

  ehfinder_reinitializerk2_2

  rk2 scheme step 2

 

  After: sym_rk2_1
  Language: fortran
  Storage: dfx
    dfy
    dfz
    dfsq
  Type: function

RK2_ReInitialize (conditional)

  ehfinder_applysymf

  select f for boundary conditions

 

  After: ehfinder_reinitializerk2_2
  Language: fortran
  Sync: f
  Type: function

RK2_ReInitialize (conditional)

  applybcs

  apply boundary conditions (symmetries)

 

  After: sym_rk2_2
  Type: group

CCTK_POSTSTEP

  ehfinder_setmask

  set the mask

 

  After: ehfinder_reinitialize
  Storage: tm_mask
  Type: group

EHFinder_SetMask

  ehfinder_setmask1

  start modifying the mask

 

  Language: fortran
  Sync: f
    eh_mask
    tm_mask
  Type: function

EHFinder_SetMask

  ehfinder_applysymall

  select both f and eh_mask for boundary conditions

 

  After: ehfinder_setmask1
  Language: fortran
  Type: function

EHFinder_SetMask

  applybcs

  apply boundary conditions (symmetries)

 

  After: ehfinder_applysymall
  Type: group

EHFinder_SetMask

  ehfinder_setmask2

  find excision boundaries

 

  After: ehfinderall_applybcs
  Language: fortran
  Sync: eh_mask
    tm_mask
  Type: function

EHFinder_SetMask

  ehfinder_applysymmask

  select eh_mask for boundary conditions

 

  After: ehfinder_setmask2
  Language: fortran
  Type: function

EHFinder_SetMask

  applybcs

  apply boundary conditions (symmetries)

 

  After: asm1
  Type: group

CCTK_INITIAL (conditional)

  ehfinder_initweights

  setup weights for simpson integration

 

  Language: fortran
  Type: function

EHFinder_SetMask

  ehfinder_setmask3

  check to see if the mask needs to be modified

 

  After: ehfinder_asm1
  Language: fortran
  Sync: eh_mask
    tm_mask
  Type: function

EHFinder_SetMask

  ehfinder_applysymmask

  select eh_mask for boundary conditions

 

  After: ehfinder_setmask3
  Language: fortran
  Type: function

EHFinder_SetMask

  applybcs

  apply boundary conditions (symmetries)

 

  After: asm2
  Type: group

EHFinder_SetMask

  ehfinder_setmask2

  find excision boundaries

 

  After: asm2
  Language: fortran
  Sync: eh_mask
    tm_mask
  Type: function

EHFinder_SetMask

  ehfinder_applysymmask

  select eh_mask for boundary conditions

 

  After: sm2
  Language: fortran
  Type: function

EHFinder_SetMask

  applybcs

  apply boundary conditions (symmetries)

 

  After: asm3
  Type: group

CCTK_POST_RECOVER_VARIABLES (conditional)

  ehfinder_init

  setup local variables

 

  Language: fortran
  Sync: f
  Type: function

Aliased Functions

 

Alias Name:         Function Name:
ApplyBCs EHFinderMask3_ApplyBCs
EHFinder_ApplySymF Sym_RK2_2
EHFinder_ApplySymMask ASM3
EHFinder_PreReInitialize EHFinder_PreReInitializePugh
EHFinder_SetMask2 SM2
Euler_PostStep Euler_PostStepPUGH
Euler_ReInitializeEvolve Euler_ReInitializeEvolvePUGH