AHFinderDirect – A Fast Apparent Horizon Finder
Jonathan Thornburg <jthorn@aei.mpg.de>
\( \)Date\( \)
Abstract
Thorn AHFinderDirect locates apparent horizons (or more generally, closed 2-surfaces with \(S^2\)
topology having any desired constant expansion) in a numerically computed slice using a direct
method, posing the apparent horizon equation as an elliptic PDE on angular-coordinate space. This
is very fast and accurate, but requires a “reasonable” initial guess. This thorn guide describes how
to use the thorn.
1 Introduction
A “marginally trapped surface” is a closed 2-surface in a slice whose congruence of future-pointing outgoing null
geodesics has zero expansion. There may be several such surfaces, some nested inside others; an “apparent
horizon” is an outermost marginally trapped surface. In terms of the usual \(3+1\) variables, an apparent
horizon satisfies the equation \begin {equation} \Theta \equiv \del _i n^i + K_\ij n^i n^j - K = 0 \label {AHFinderDirect/eqn-horizon} \end {equation} where \(n^i\) is the outward-pointing unit normal to the apparent horizon,
and \(\del _i\) is the covariant derivative operator associated with the 3-metric \(g_\ij \) in the slice. (See [?] for a
derivation of equation \((\ref {AHFinderDirect/eqn-horizon})\).) (Optionally, you can replace the right hand side of \((\ref {AHFinderDirect/eqn-horizon})\) by any specified nonzero
constant, i.e. you can find a surface of constant (in general nonzero) expansion.; this is dicsussed in
section 4.8.)
Thorn AHFinderDirect finds an apparent horizon by numerically solving equation \((\ref {AHFinderDirect/eqn-horizon})\). It requires as input
the usual Cactus 3-metric \(g_\ij \) and extrinsic curvature \(K_\ij \), (and optionally the conformal factor \(\psi \) if the
StaticConformal metric semantics are used), and produces as output the Cactus \((x,y,z)\) coordinates of
a large number of points on the apparent horizon, together with some auxiliary information like
the apparent horizon area and centroid position, and the irreducable mass associated with the
area.
Besides this thorn guide, the other main sources of information on AHFinderDirect are the comments in the
param.ccl file, the paper [?], and to a lesser extent the paper [?]. As a courtesy, I ask that both
these papers be cited in any published research which uses this thorn, or which uses code from this
thorn.
2 What AHFinderDirect Needs
There are some restrictions on the spacetime, or more precisely on each slice where you want to find apparent
horizons, which are necessary in order for AHFinderDirect to work:
-
AHFinderDirect requires that the Cactus geometry (\(g_{ij}\), \(K_{ij}\), and optionally \(\psi \)) be nonsingular in a
neighborhood of the apparent horizon. In particular, this means that it quite certainly will not work
for spacetimes/slicings which have a singular geometry on the horizon, such as Schwarzschild/Schwarzschild
and Kerr/Boyer-Lindquist.
-
Less obviously, this also means that if there is a singularity in the geometry somewhere near the
apparent horizon, then you need to have a high enough Cactus 3-D grid resolution that the geometry
interpolation doesn’t “see” the singularity. (If AHFinderDirect “sees” the singularity, it may
“just” fail to find the horizon, and/or it may report that the interpolated \(g_{ij}\) fails to be positive definite
or even contains NaNs.)
-
At the moment AHFinderDirect and the Cactus interpolators don’t know how to avoid an
excised region, so if the apparent horizon (or any trial horizon surface as the algorithm is iterating
towards the apparent horizon) gets too close to an excised region, you’ll get garbage results as the
interpolator tries to interpolate data from the excised region. I plan to fix this sometime soon.
-
AHFinderDirect requires that any apparent horizon it’s going to (try to) find must be a
“Strahlkörper” (literally “ray body”, or more commonly “star-shaped region”) relative to some local
coordinate origin (which you must specify). A Strahlkörper is defined by Minkowski ([?, p. 108])
as
a region in \(n\)-dimensional Euclidean space containing the origin and whose surface, as seen
from the origin, exhibits only one point in any direction.
In other words, using polar spherical coordinates relative to the local coordinate origin, the apparent
horizon’s shape must be parameterizable as \(r = h(\text {angle})\) for some single-valued function \(h: S^2 \to \Re ^+\). (AHFinderDirect uses
precisely this parameterization.)
There are also some restrictions on your Cactus configuration and run; here’s what works and what doesn’t:
-
I strongly recommend using a current-CVS checkout of the Cactus flesh and of all relevant thorns.
I haven’t tested AHFinderDirect at all with older versions of the flesh or other thorns.
-
AHFinderDirect works fine with the PUGH unigrid driver and with the Carpet
mesh-refinement driver. So far as I know it’s never been tested with any other driver.
-
AHFinderDirect works fine in single- or multi-processor Cactus runs.
-
Obviously, your Cactus configuration must include AHFinderDirect, and your ActiveThorns
parameter(s) must activate it.
-
AHFinderDirect inherits from the other thorns (strictly speaking, implementations) listed in
table 1, so you’ll need them (or more precisely some thorns providing them) in your configuration
and activated, too.
| Implementation | Typically provided by Thorn |
|
|
| Grid | CactusBase/CartGrid3d |
| IO | CactusBase/IOUtil |
| ADMBase | CactusEinstein/ADMBase |
| StaticConformal | CactusEinstein/StaticConformal |
| SpaceMask | CactusEinstein/SpaceMask |
| SphericalSurface | AEIThorns/SphericalSurface |
Table 1: This table lists all the other implementations from which AHFinderDirect inherits, and
the thorns which typically provide these implementations.
-
Grid::domain = "full", "bitant", "quadrant", and "octant" are supported. Alas, at present rotating
(or more precisely nonlocal) symmetry boundary conditions aren’t supported.
-
The ADMBase::metric_type values "physical" and "static conformal" are supported; for the latter
you must have storage turned on for at least the conformal factor StaticConformal::psi. (The Cactus
3-D grid functions for 1st and 2nd derivatives of psi aren’t used.)
-
AHFinderDirect uses the CCTK_InterpGridArrays() Cactus global (multi-processor grid array)
interpolator API; this is provided by PUGHInterp or CarpetInterp (so you must have the appropriate
one of these thorns compiled in and activated). CCTK_InterpGridArrays() in turn uses the new
CCTK_InterpLocalUniform() processor-local interpolator API; AHFinderDirect uses various options in
this API which at present are only supported by thorn AEILocalInterp (so you must have this thorn
compiled in and activated)
-
AHFinderDirect uses various Cactus reduction APIs to coordinate multi-processor horizon finding, so
(even if you’re only going to run on a single processor) you must have a reduction thorn like
PUGHReduce or CarpetReduce compiled in and activated.
-
At present only a few of AHFinderDirect’s parameters are steerable. (This is actually quite easy to fix; I
just haven’t gotten around to it yet.)
-
I think AHFinderDirect will “work” with checkpoint/restart, but I haven’t tested this yet. Here “work”
means the restart will be like starting a new run, in that AHFinderDirect will set the initial guess for
each horizon in a start-of-a-new-run manner. Alas, it will also write a new BH_diagnostics file for
each horizon found, overwriting any existing BH_diagnostics files. This is a bug, which I
plan to fix soon (the right behavior is/will be to append to the existing BH_diagnostics
file).
AHFinderDirect can pass information to the rest of Cactus in several ways; these are described in detail in
section 4.7.
3 Obtaining and Compiling AHFinderDirect
You should be able to obtain the source code for this thorn via the usual procedures for anonymous git checkout;
at present it lives in the EinsteinAnalysis arrangement.
This thorn is written primarily in C++, calling C and Fortran 77 numerical
libraries. In
theory the code should be quite portable to modern C++ compilers, but in practice I’ve had a
number of portability problems with various compilers. See the “Code Notes” and “Compiler Notes”
sections in the top-level README file for details and lists of compilers currently known to be ok or
not.
By default AHFinderDirect doesn’t use any external libraries. However, if HAVE_DENSE_JACOBIAN__LAPACK is
defined in src/include/config.h, then AHFinderDirect uses the LAPACK library for solving linear
equations. In this case you need to configure Cactus with LAPACK=yes. See the top-level README and
README.library files for details on this.
4 AHFinderDirect Parameters
This thorn has lots of parameters, but most of them have reasonable default values which you probably won’t
need to change. Here I describe the parameters which you are likely to want to at least look at, and possibly set
explicitly.
Note that all of the “[\(n\)]” parameters are Cactus array parameters, which you need to specify separately in your
parameter file for each apparent horizon. IMPORTANT: Apparent horizons are numbered starting at
1, not 0! The example in section 8 should make this clear.
4.1 Overall Parameters
-
find_every
-
This is an integer parameter specifying how often AHFinderDirect should try to find apparent
horizons: If \(\verb |find_every| = 0\), AHFinderDirect is a no-op. If \(\verb |find_every| \ne 0\), AHFinderDirect tries to find apparent horizons
each find_every time steps.
The default value is 1, i.e. AHFinderDirect tries to find apparent horizons at every time step.
-
N_horizons
-
How many apparent horizons do you want to find in each slice? Typical values are 1 (the default), 2,
or 3.
This thorn numbers the apparent horizons from 1 to N_horizons inclusive. There are a
number of other parameters (described below) which you need to set for of these each apparent
horizons.
Note that N_horizons sets the number of apparent horizons you want to find in the Cactus 3-D
numerical grid, not in the whole spacetime. For example, if you are simulating (say) Misner data
with Grid::domain = "bitant", with the two throats at (say) roughly \(z = \pm 1\), then you should set
N_horizons = 1 to find those two apparent horizons, since you’re only finding one apparent horizon
within the numerical grid. If you also want to search for a common apparent horizon surrounding
both black holes, then you should set N_horizons = 2, since you’re finding at most 2 apparent
horizons within the numerical grid.
-
verbose_level
-
This controls how verbose this thorn is in printing informational (non-error) messages describing what it’s
doing. In order from tersest to most verbose, the allowable values are
-
"no output"
-
Don’t print anything.
-
"physics highlights"
-
Print only a single line each time AHFinderDirect runs, giving which horizons were found.
-
"physics details"
-
Print two lines for each horizon found, giving the horizon area, centroid position, and
irreducible mass. This is the default.
-
"algorithm highlights"
-
Also print a single line for each Newton iteration giving the 2-norm and \(\infty \)-norm of the \(\Theta (h)\) function
defined by equation \((\ref {AHFinderDirect/eqn-horizon})\).
-
"algorithm details"
-
Print lots of detailed messages tracing what the code is doing.
-
"algorithm debug"
-
Print even more detailed messages tracing what the code is doing, mainly useful for debugging
purposes.
4.2 Choosing the Local Coordinate Origin for each Apparent Horizon
For each apparent horizon you want to find, you need to specify the Cactus \((x,y,z)\) coordinates of a local coordinate
system origin. As described in section 2, each apparent horizon must be a Strahlkörper with respect to its local
coordinate system origin.
You specify the local coordinate system origin for each horizon with the (Cactus array) parameters
-
| origin_x[\(n\)] |
| origin_y[\(n\)] |
| origin_z[\(n\)] |
-
These all default to 0.0. In practice, you should set these parameters to be somewhere reasonably
close to your best guess for the center of each apparent horizon. These aren’t too critical: being off
by 1/4 of the horizon radius is no problem, and – assuming the algorithm still converges – even 1/2
of the horizon radius only slows the convergence by an extra iteration or two. But poor values of
these parameters do make the algorithm more likely to fail to converge.
At present the local coordinate origin is fixed once you set it; there’s no provision
for it to move to track a moving black hole. I hope to add such a provision
soon.
4.3 Specifying the Initial Guess
AHFinderDirect requires an initial guess for the apparent horizon’s coordinate position and shape (that is, for
the \(h(\text {angle})\) function defined in section 2), for each apparent horizon you want to find. Unlike some other apparent
horizon finders (eg. the curvature flow method in AHFinder), for AHFinderDirect there’s no
restriction on whether the initial guess is inside, outside, or crossing the actual apparent horizon: the
only important thing is that it should be “close”. Just how close the initial guess needs to be for
AHFinderDirect to find the (a) apparent horizon depends on the slice and the coordinates, but as a general
rule of thumb any initial guess that’s within 1/3 to 1/2 of the mean horizon radius will probably
work.
The “initial guess” specification is used the first time we try to find any given apparent horizon, and also any
succeeding time when the most recent attempt to find this apparent horizon failed. If we succeed in finding a
given apparent horizon, than that apparent horizon position is automatically reused as the initial guess the next
time we try to find the same apparent horizon; in this case the explicit “initial guess” specification is
ignored.
There are a number of parameters for specifying the initial guess:
-
initial_guess_method[\(n\)]
-
This sets what type of the initial guess is used for each apparent horizon
position. There are several possibilities, most with their own sets of
subparameters: \(^,\)
-
"read from file"
-
This reads the initial-guess \(h(\text {angle})\) function from a data file. The file format is currently hard-wired
to be that written with file_format = "ASCII (gnuplot)" (see below). The subparameter
initial_guess__read_from_named_file__file_name specifies the file name.
-
"Kerr/Kerr"
-
This sets the initial guess to the analytically-known apparent horizon position in a Kerr spacetime in
Kerr coordinates. This is a coordinate sphere of radius \((1 + \sqrt {1 - a^2}) m\). There are subparameters
-
| initial_guess__Kerr_Kerr__x_posn[\(n\)] |
| initial_guess__Kerr_Kerr__y_posn[\(n\)] |
| initial_guess__Kerr_Kerr__z_posn[\(n\)] |
-
to set the position of the Kerr black hole (note this position is in global Cactus coordinates,
not relative to the local coordinate origin), and
-
| initial_guess__Kerr_Kerr__mass[\(n\)] |
| initial_guess__Kerr_Kerr__spin[\(n\)] |
-
to set its mass and spin.
-
"Kerr/Kerr-Schild"
-
This sets the initial guess to the analytically-known apparent horizon position in a Kerr spacetime
in Kerr-Schild coordinates. This is a coordinate ellipsoid with radia (semi-major axes)
\begin {equation} \renewcommand {\arraystretch }{2.0} \begin {array}{lclcl} r_z & = & (1 + \sqrt {1 - a^2}) m \\ r_x = r_y & = & r_z \sqrt {1 + \left (\dfrac {am}{r_z}\right )^2} & = & \sqrt {\dfrac {2 r_z}{m}} \, m \end {array} \end {equation}
-
| initial_guess__Kerr_KerrSchild__x_posn[\(n\)] |
| initial_guess__Kerr_KerrSchild__y_posn[\(n\)] |
| initial_guess__Kerr_KerrSchild__z_posn[\(n\)] |
-
(note this position is in global Cactus coordinates, not relative to the local coordinate
origin), and
-
| initial_guess__Kerr_KerrSchild__mass[\(n\)] |
| initial_guess__Kerr_KerrSchild__spin[\(n\)] |
-
to set its mass and spin.
-
"coordinate sphere"
-
This sets the initial guess to a coordinate sphere; there are subparameters
-
| initial_guess__coord_sphere__x_center[\(n\)] |
| initial_guess__coord_sphere__y_center[\(n\)] |
| initial_guess__coord_sphere__z_center[\(n\)] |
-
(note this position is in global Cactus coordinates, not relative to the local coordinate
origin), and
-
initial_guess__coord_sphere__radius[\(n\)]
-
to set the radius.
-
"coordinate ellipsoid"
-
This sets the initial guess to a coordinate ellipsoid; there are subparameters
-
| initial_guess__coord_ellipsoid__x_center[\(n\)] |
| initial_guess__coord_ellipsoid__y_center[\(n\)] |
| initial_guess__coord_ellipsoid__z_center[\(n\)] |
-
(note this position is in global Cactus coordinates, not relative to the local coordinate
origin), and
-
| initial_guess__coord_ellipsoid__x_radius[\(n\)] |
| initial_guess__coord_ellipsoid__y_radius[\(n\)] |
| initial_guess__coord_ellipsoid__z_radius[\(n\)] |
-
to set the radia (semimajor axes).
4.4 I/O Parameters for the Apparent Horizon Shape(s)
The main output of this thorn is the computed horizon shape function \(h({\rm angle})\), and correspondingly the \((x,y,z)\) coordinate
positions of the apparent-horizon-surface (angular) grid points. There are several parameters controlling if, how
often, and how these should be written to data files:
-
output_h_every
-
As described in section 4.1, AHFinderDirect will try to find the apparent horizon(s) every
find_every time steps. However, you can control how often (if at all) the apparent horizon shape(s)
are written to data files: this is only done if output_h_every is nonzero, and the Cactus time step
number cctk_iteration is an integral multiple of this parameter (output_h_every).
-
file_format
-
This specifies the file format for horizon-shape (and other angular-grid-function) data files. Unfortunately,
at the moment only a single format is implemented,
-
"ASCII (gnuplot)"
-
This is a simple ASCII format designed for easy plotting with gnuplot:
-
AHFinderDirect writes a separate data file for each Cactus time step and for each
apparent horizon found. By default these are all written in to the IOUtil::out_dir
directory; see h_directory (below) to change this.
-
The time step number and the apparent horizon number are both encoded in the file name;
the actual file name is given by a printf() format "%s/%s.t%d.ah%d.%s", where
-
the first %s is the directory set by the IO::out_dir and/or h_directory parameters
(see below)
-
the second %s is the base file name set by the h_base_file_name parameter (see
below)
-
the first %d is the Cactus time step number
-
the second %d is the apparent horizon number
-
the third %s is the file name extension, set by the
ASCII_gnuplot_file_name_extension parameter; this defaults to "gp"
-
Comment lines begin with #.
-
Patches are separated by 2 blank lines; rows of apparent-horizon points within a patch are
separated by single blank lines.
-
Each apparent-horizon-surface point is described by a single line, containing the
whitespace-separated fields
-
Two “unwrapped” angular coordinates in degrees, representing a point on \(S^2\).
-
The \(h\) value, giving the radius of the apparent horizon surface at that angle.
-
The corresponding Cactus \((x,y,z)\) coordinates.
See section 6 for a discussion of visualization for these and other AHFinderDirect output
files.
-
h_directory
-
This specifies the directory in which the \(h\) data files are to be written. If it doesn’t already exist, this
directory is created before writing the data files. This parameter defaults to the value of the IO::out_dir
parameter.
-
h_base_file_name
-
This specifies the base file name for \(h\) data files, as described above. This defaults to ”h”.
-
ASCII_gnuplot_file_name_extension
-
This specifies the file name extension for \(h\) data files, as described above. This defaults to
”gp”.
4.5 Parameters for the “BH_diagnostics” Files
As well as the apparent horizon shape files, this thorn can also write files giving time series of various
diagnostics. These are controlled by the following parameters:
-
output_BH_diagnostics
-
If this Boolean parameter is set to true, AHFinderDirect will write a “black hole diagnostics” file for
each distinct apparent horizon found (up to N_horizons files in all). Each such file contains a time
series of various diagnostics for all time steps when the corresponding apparent horizon was
found. The file format is again a simple ASCII format designed for easy plotting with gnuplot:
-
The apparent horizon number is encoded in the file name; the actual file name is given by a printf()
format "%s/%s.ah%d.%s", where
-
the first %s is the directory set by the IO::out_dir and/or BH_diagnostics_directory
parameters (see below)
-
the second %s is the base file name set by the BH_diagnostics_base_file_name parameter
(see below); this defaults to "BH_diagnostics"
-
the %d is the apparent horizon number
-
the third %s is the file name extension, set by the BH_diagnostics_file_name_extension
parameter; this defaults to "gp"
-
The file begins with a block of header comments (lines begining with #) describing the data
fields.
-
Each time this apparent horizon is found, a single line is appended to the data file, containing various
whitespace-separated fields. The the precise list of fields, see the header comments, or see the
function output() in src/driver/BH_diagnostics.cc. As of this writing the fields are:
-
the Cactus iteration number cctk_iteration
-
the Cactus time coordinate cctk_time
-
the Cactus \((x,y,z)\) coordinates of the apparent horizon centroid
-
the minimum, maximum, and mean coordinate radia of the apparent horizon about the
local coordinate origin
-
the minimum and maximum Cactus \(x\), \(y\), and \(z\) coordinates of the apparent horizon surface
-
the proper circumferences of the apparent horizon in the \(xy\), \(xz\), and \(yz\) local-coordinate planes
-
the \(xz/xy\) and \(yz/xy\) ratios of the proper circumferences
-
the proper area of the apparent horizon, \(A\)
-
the irreducible mass of the apparent horizon, \(\sqrt {A/16\pi }\)
-
the areal radius of the apparent horizon, \(\sqrt {A/4\pi }\)
-
BH_diagnostics_directory
-
This specifies the directory in which the black hole diagnostics data files are to be written. If it doesn’t
already exist, this directory is created before writing the data files. This parameter defaults to the value of
the IO::out_dir parameter.
-
BH_diagnostics_base_file_name
-
This specifies the base file name for black hole diagnostics data files, as described above. This defaults to
"BH_diagnostics".
-
BH_diagnostics_file_name_extension
-
This specifies the file name extension for black hole diagnostics data files, as described above. This defaults
to "gp".
4.6 (Excision) Mask Parameters
This thorn can optionally set a mask grid function (or functions) at each point of the Cactus grid,
to indicate where that point is with respect to the apparent horizon(s). This is usually used for
excision.
-
| set_mask_for_all_horizons |
| set_mask_for_individual_horizon[\(n\)] |
-
These Boolean parameters control whether AHFinderDirect should set a mask grid function(s):
If the (C) expression set_mask_for_all_horizons || set_mask_for_individual_horizon[i]
is true, then AHFinderDirect will set a mask grid function(s) for apparent horizon \(i\). All these
parameters default to false (don’t set a mask).
If any of these parameters is set to true, you almost certainly also need to set the Boolean parameter
SpaceMask::use_mask to true to to turn on storage for the mask grid function(s)!
If it’s setting a mask(s), AHFinderDirect partitions the Cactus grid into 3 regions: an “inside”, a “buffer”,
and an “outside”. Typically the inner region is excised, but AHFinderDirect doesn’t itself do this: It just sets
the mask(s); you need to use some other thorn(s) to do the actual excision.
The 3 regions are defined as follows: For a grid point a distance \(r[i]\) from horizon \(i\)’s local coordinate origin, with
horizon \(i\)’s radius in this same direction (again, measured from its local coordinate origin) being
\(r_{\text horizon}[i]\), the regions are
defined by \begin {equation} \renewcommand {\arraystretch }{1.333} \begin {tabular}{l@{~}lll@{~}lll} $r[i] \le r{ ext{r}}[i]$ & \text {for some $i$} & & & & $\Rightarrow $ & \text {inner} \\ $r[i] > r_{\text {r}}[i]$ & \text {for all $i$} & \text {and} & $r[i] \le r_{\text {r}}[i]$ & \text {for some $i$} & $\Rightarrow $ & \text {buffer} \\ $r[i] > r_{\text {r}}[i]$ & \text {for all $i$} & & & & $\Rightarrow $ & \text {outer} \end {tabular} \end {equation} where \begin {equation} \renewcommand {\arraystretch }{1.333} \begin {array}{lcl} r_{\text {r}} & = & \verb |mask_radius_multiplier| \times r_{\text {n}} \,\,+\,\, \verb |mask_radius_offset| \times {\Delta x}_{\text {e}} \\ r_{\text {r}} & = & r_{\text {r}} \,\,+\,\, \verb |mask_buffer_thickness| \times {\Delta x}_{\text {e}} \end {array} \label {AHFinderDirect/eqn-r-inside-outside} \end {equation} and where \({\Delta x}_{\text {e}}\) is the base-grid Cactus grid spacing (more precisely, the geometric mean of the base grid’s \(x\), \(y\), and
\(z\) Cactus grid spacings) .
-
| mask_radius_multiplier |
| mask_radius_offset |
| mask_buffer_thickness |
-
These parameters are used to define the radia \(r_{\text {r}}\) and \(r_{\text {r}}\) in equation \((\ref {AHFinderDirect/eqn-r-inside-outside})\) above.
Note that the sign convention here is that mask_radius_multiplier is multiplied by the horizon
radius, then mask_radius_offset (scaled by the Cactus grid spacing) is added. Thus for use
with excision (where the inner region – which will be excised – must be somewhat inside the
horizon), mask_radius_multiplier should be a positive real number slightly less than 1.0, and/or
mask_radius_offset a negative real number.
The default values for these parameters are
mask_radius_multiplier = 0.8
mask_radius_offset = -5.0
mask_buffer_thickness = 5.0
-
mask_is_noshrink
-
This Boolean parameter specifies whether the inside and buffer regions should be prevented from ever
shrinking during a time evolution (this is the default), or whether they should be set independently from
one time step to the next (and thus allowed to either grow or shrink). More precisely, once a given grid
point has been classified as inside, buffer, or outside, AHFinderDirect executes the following
algorithm:
-
inside
-
| \(\verb |mask| \assign \verb |inside_value|\)
|
-
buffer
-
| if | (mask_is_noshrink && (\(\verb |mask| = \verb |inside_value|\)))
|
| # this point was previously inside \(\Rightarrow \) no-op here |
| else | \(\verb |mask| \assign \verb |buffer_value|\) |
-
outside
-
| if | (mask_is_noshrink && ((\(\verb |mask| = \verb |inside_value|\)) || (\(\verb |mask| = \verb |buffer_value|\)))
|
| # this point was previously inside or buffer \(\Rightarrow \) no-op here |
| else | \(\verb |mask| \assign \verb |outside_value|\) |
-
min_horizon_radius_points_for_mask
-
By default, AHFinderDirect sets the mask for each apparent horizon found. If we’re using mesh
refinement, it’s possible for an apparent horizon to be found on a coarse grid, and the masked region to be
only a few grid points across on a fine grid. This causes some other Cactus thorns (eg. LegoExcision) to
crash. :(
This parameter can be used to avoid this problem: For each apparent horizon that it finds,
AHFinderDirect only sets the mask on a given grid if \begin {equation} r_{\text {inner},\min } \ge \verb |min_horizon_radius_points_for_mask| * {\Delta x}_{\text {current},\max } \end {equation} where \(r_{\text {inner},\min }\) is the minimum over all angles of \(r_{\text {r}}\) as
defined by equation \((\ref {AHFinderDirect/eqn-r-inside-outside})\), and \({\Delta x}_{\text {current},\max }\) is the maximum of the Cactus \(x\), \(y\), and \(z\) grid spacings on the current Cactus
grid.
If this condition isn’t satisfied, then AHFinderDirect skips setting the mask for this apparent horizon,
just as if this apparent horizon wasn’t found. (Note that all other processing for an apparent horizon being
found is still done, including writing output files, using the apparent horizon shape as the initial guess for
the next time step’s apparent-horizon finding, etc.; it’s only the mask processing for this horizon (at this
time step) that’s skipped.)
AHFinderDirect supports two types of mask grid functions; the following two Boolean parameters choose
which of them you want to set; you can set either or even both of these:
-
set_old_style_mask
-
This parameter (default true) specifies an old-style excision mask, one stored in a CCTK_REAL
Cactus grid function. (The AHFinder apparent horizon finder uses this type of mask.)
-
set_new_style_mask
-
This parameter (default false) specifies a new-style excision mask, one stored in a specified bit
field of a CCTK_INT Cactus grid function. The bit field is specified by its name, as registered
with the SpaceMask thorn. We plan to eventually convert all Cactus excision (and other uses
of mask grid functions) to this scheme, but at the moment not much code supports it. Note that
AHFinderDirect doesn’t itself create/register any bit fields or state names with SpaceMask –
you must arrange for some other thorn(s) to do this.
For an old-style mask, the following parameters specify the mask grid function and how it should be
set:
-
old_style_mask_gridfn_name
-
This parameter specifies the mask grid function’s name.
-
| old_style_mask_inside_value |
| old_style_mask_buffer_value |
| old_style_mask_outside_value |
-
If an old-style mask is to be set in the corresponding regions, these parameters specify the values
to which it should be set. These are all CCTK_REAL values.
For an new-style mask, the following parameters specify the mask grid function and how it should be
set:
-
| new_style_mask_gridfn_name |
| new_style_mask_bitfield_name |
-
These parameters specify the mask grid function’s name and the bitfield name within it.
-
| new_style_mask_inside_value |
| new_style_mask_buffer_value |
| new_style_mask_outside_value |
-
If an new-style mask is to be set in the corresponding regions, these parameters specify the values to
which it should be set. These are all character-string state names, as registered with the SpaceMask
thorn.
Note that AHFinderDirect doesn’t itself register any bitfields or states with SpaceMask – you must arrange
for some other thorn(s) to do this before AHFinderDirect tries to find the horizon(s).
If AHFinderDirect sets a mask or masks, this happens in the same schedule bin(s) as the horizon finding.
More precisely, AHFinderDirect creates two schedule groups for this purpose:
-
The schedule group group_for_mask_stuff is scheduled to run just after the horizon is found.
-
The schedule group group_where_mask_is_set is scheduled inside the schedule group
group_for_mask_stuff.
-
The actual setting of the mask is scheduled inside the schedule group group_where_mask_is_set.
Thorn PreviousMask uses these schedule groups to keep a “previous” as well as a “current” mask. See that
thorn’s thorn guide for further details.
4.7 Communicating with Other Thorns
Besides the data files it writes, AHFinderDirect currently has three ways to communicate with other Cactus
thorns:
-
AHFinderDirect can set a mask grid function(s) based on the (a) horizon’s shape; other thorns
may then use this for excision or other purposes. AHFinderDirect supports both the old-style
(CCTK_REAL) mask (compatible with AHFinder) or the new-style (CCTK_INT) mask bit-fields
defined by SpaceMask; you can even use both styles simultaneously.
-
AHFinderDirect can announce a selected horizon’s centroid position to another thorn (typically
DriftCorrect, which uses this to adjust its corotating shift vector). This uses the new
function-aliasing version of DriftCorrect, not the old version which worked with an auxiliary thorn
AHFSetDCCentroid.
-
AHFinderDirect provides a set of aliased functions which any other thorn(s) can call to find out
the shape of a specified horizon.
-
AHFinderDirect can store information about the horizon(s) it finds in the SphericalSurface
variables for other thorns to use.
AHFinderDirect’s mask features are described in section 4.6; the other communication mechanisms are
described in the following subsections.
4.7.1 Parameters for Announcing a Horizon Centroid to Other Thorns
This thorn can optionally announce the centroid of a specified apparent horizon to another thorn
(typically DriftCorrect) each time that apparent horizon is found. This is controlled by the following
parameter:
-
which_horizon_to_announce_centroid
-
This is an integer parameter which defaults to 0 (which means not to announce any centroid). If
it’s set to a nonzero integer, that specifies the horizon number to have its centroid announced.
4.7.2 Aliased Functions to Provide Horizon-Shape Information
AHFinderDirect provides the following aliased functions to allow other thorns to find out about the horizons.
Each function returns a status code which is \(\ge 0\) for ok, or negative for an error.
#
# This function returns the local coordinate origin for a given horizon.
#
CCTK_INT FUNCTION HorizonLocalCoordinateOrigin \
(CCTK_INT IN horizon_number, \
CCTK_REAL OUT origin_x, CCTK_REAL OUT origin_y, CCTK_REAL OUT origin_z)
#
# The following function queries whether or not the specified horizon
# was found the most recent time AHFinderDirect searched for it.
# The return value is:
# 1 if the horizon was found
# 0 if the horizon was not found
# negative for an error
#
CCTK_INT FUNCTION HorizonWasFound(CCTK_INT IN horizon_number)
#
# The following function computes the horizon radius in the direction
# of each (x,y,z) point, or -1.0 if this horizon wasn’t found the most
# recent time AHFinderDirect searched for it. More precisely, for each
# (x,y,z), consider the ray from the local coordinate origin through
# (x,y,z). This function computes the Euclidean distance between the
# local coordinate origin and this ray’s intersection with the horizon,
# or -1.0 if this horizon wasn’t found the most recent time AHFinderDirect
# searched for it.
#
# If this function is to be used in a multiprocessor run on a horizon
# which was found on some other processor, the parameter
# AHFinderDirect::always_broadcast_horizon_shape
# must be set to true to get the correct answer.
#
CCTK_INT FUNCTION HorizonRadiusInDirection \
(CCTK_INT IN horizon_number, \
CCTK_INT IN N_points, \
CCTK_REAL IN ARRAY x, CCTK_REAL IN ARRAY y, CCTK_REAL IN ARRAY z, \
CCTK_REAL OUT ARRAY radius)
4.7.3 Storing Horizon-Shape Information in the SphericalSurface Variables
SphericalSurface (in the AEIThorns arrangement) defines a set of generic grid arrays which describe
“spherical surfaces”. AHFinderDirect can optionally store information about the horizons it finds in the
SphericalSurface variables. This is controlled by the following parameters:
-
which_surface_to_store_info[\(n\)]
-
This parameter should be set to the SphericalSurface surface number into which information on
a given AHFinderDirect horizon should be stored, or to -1 to skip storing the information. It
defaults to -1 for each horizon.
Note that SphericalSurface numbers surfaces starting from 0, whereas AHFinderDirect
numbers horizons starting from 1!
At present, if multiple AHFinderDirect horizons specify the same SphericalSurface surface,
the highest-numbered horizon will “win”, i.e. it will overwrite the data from any lower-numbered
horizons.
4.8 Other Parameters
-
| run_at_CCTK_ANALYSIS |
| run_at_CCTK_POSTSTEP |
| run_at_CCTK_POSTINITIAL |
| run_at_CCTK_POST_RECOVER_VARIABLES |
-
These parameters (which default to true, false, false, and true respectively) control
which schedule bins AHFinderDirect runs in. Historically, AHFinderDirect ran in
CCTK_ANALYSIS, and that’s still the default, but these parameters allow you to change this so it
runs in CCTK_POSTSTEP and/or CCTK_POSTINITIAL instead. (You can even run in all three
bins if you want!)
In general we need to run at CCTK_POST_RECOVER_VARIABLES, since
-
parameters may have been steered at recovery, so we may need to find a new horizon or
horizons, and
-
we need to set the mask again to make sure it’s correct right away (since our next regular
horizon-finding may not be until some time steps later)
Therefore the run_at_CCTK_POST_RECOVER_VARIABLES parameter should probably be left at its default
setting of true.
-
| geometry_interpolator_name |
| geometry_interpolator_pars |
-
These parameters control the (3-D) “geometry interpolation” of the spacetime geometry (\(g_{ij}\) and \(K_{ij}\), or their
StaticConformal equivalents) to the apparent horizon position. The defaults are set to use a quadratic
Hermite interpolator. This works fairly well, but because of the interpolator molecule size you must use
\(\verb |driver::ghost_size| \ge 2\).
If you want to get very high accuracy from AHFinderDirect, then you should use a cubic Hermite
geometry interpolator, by setting
AHFinderDirect::geometry_interpolator_pars = "
order=3
boundary_off_centering_tolerance={1.0e-10 1.0e-10 1.0e-10 1.0e-10 1.0e-10 1.0e-10}
boundary_extrapolation_tolerance={0.0 0.0 0.0 0.0 0.0 0.0}
"
Assuming perfectly accurate geometry variables in the 3-D Cactus grid, this will make AHFinderDirect
(very) roughly an order of magnitude more accurate. However, the larger molecule size will make it about a
factor of 2–3 slower, and will also require that you set \(\verb |driver::ghost_size| \ge 3\). The sample parameter file par/Kerr-order3.par
shows an example of this.
-
N_zones_per_right_angle[\(n\)]
-
This parameter sets the angular resolution used to compute each patch. The units are the number of
angular grid zones per right angle. The default is 18, i.e. a 5 degree angular resolution. There’s no
problem with this parameter varying from one horizon to another, but for simplicity it should be
even.
For any horizon which is close to spherical about its local coordinate origin, you can lower this parameter
to make AHFinderDirect run faster (typical run-times scale roughly as the cube of this parameter); 6 is
about the minimum reasonable value.
For any horizon which is highly non-spherical about its local coordinate origin, you can raise
this parameter to get better resolution; 30 should be enough for even a highly non-spherical
horizon.
-
max_allowable_horizon_radius[\(n\)]
-
This parameter gives the maximum mean-coordinate-radius which any given
trial surface may have in the course of trying to solve the apparent horizon
equation.
In particular, if any trial surface has a mean coordinate radius which exceeds this parameter,
AHFinderDirect gives up and deems this apparent horizon to be “not found”.
This parameter defaults to \(10^{10}\) (effectively \(+\infty \)) for each apparent horizon. You can set it to a smaller value to
make AHFinderDirect a bit more efficient, or (probably more important in practice) to stop
AHFinderDirect from iterating off the edge of the grid if this causes problems with interpolation or
boundary conditions.
-
max_allowable_Theta
-
This parameter gives the maximum \(\|\Theta \|_\infty \) which any given trial surface may have in the course of trying to solve
the apparent horizon equation. In particular, if any trial surface has \(\|\Theta \|_\infty \) exceeding this parameter,
AHFinderDirect gives up and deems this apparent horizon to be “not found”. This parameter defaults
to \(10^{10}\) (effectively \(+\infty \)) for each apparent horizon.
-
surface_expansion[\(n\)]
-
This parameter (which defaults to 0.0) sets the expansion of each surface. With the default setting this
thorn solves \((\ref {AHFinderDirect/eqn-horizon})\) to find apparent horizons. With other settings of this parameter this thorn can be used to
find “surfaces of constant expansion”; these may be useful for excision, wave extraction, or other purposes
([?]).
To help in choosing the value(s) of the surface_expansion[\(n\)] parameter, figure 1 (from [?]), shows
the expansion of \(r = \text {constant}\) surfaces in an Eddington-Finkelsteon slice of the unit-mass Schwarzschild
spacetime.
5 Monitoring AHFinderDirect’s Status
There are two primary ways of monitoring what AHFinderDirect is doing during a Cactus run: the
BH_diagnostics files and the CCTK_INFO messages written to the Cactus standard output:
The BH_diagnostics files are described in detail in section 4.5. These files are written and “flushed” at each
time step, so they’re always up-to-date.
During the apparent-horizon–finding process, AHFinderDirect writes various CCTK_INFO messages describing
the convergence of the iterative solution of the apparent horizon equation 1 on each processor. In particular, if
verbose_level is set to "algorithm highlights" or a more verbose setting (cf. section 4.1), then
AHFinderDirect writes CCTK_INFO messages like these:
INFO (AHFinderDirect): proc 0/horizon 1:it 1 r_grid=0.595 ||Theta||=1.1e-01
INFO (AHFinderDirect): proc 0/horizon 1:it 2 r_grid=0.614 ||Theta||=7.2e-02
INFO (AHFinderDirect): proc 0/horizon 1:it 3 r_grid=0.632 ||Theta||=2.9e-02
INFO (AHFinderDirect): proc 0/horizon 1:it 4 r_grid=0.642 ||Theta||=9.9e-04
INFO (AHFinderDirect): proc 0/horizon 1:it 5 r_grid=0.642 ||Theta||=7.9e-07
INFO (AHFinderDirect): proc 0/horizon 1:it 6 r_grid=0.642 ||Theta||=7.2e-13
INFO (AHFinderDirect): AH 1/2: r=0.660716 at (0.000000,0.000000,1.127434)
INFO (AHFinderDirect): AH 1/2: area=338.0473838 m_irreducible=2.59330658
INFO (AHFinderDirect): writing h to "misner.h.t0.ah1.gp"
Here r_grid is a rough estimate of the mean radius of the trial surface at each iteration, and ||Theta|| is the
infinity-norm of \(\Theta \), the left hand side of the apparent horizon equation 1 over the surface. Once the apparent
horizon has been found (||Theta|| is sufficiently small), then AHFinderDirect prints its mean
radius,
centroid position, area, and irreducible mass.
6 Visualization
There are several ways to visualize AHFinderDirect’s output:
The simplest is to plot various quantities from the BH_diagnostics files (described in detail in section 4.5). For
example, using gnuplot (http://www.gnuplot.info), you can plot a graph of the surface area of horizon #4 as
a function of coordinate time, with the command
plot ’BH_diagnostics.ah4.gp’ using 2:26 with points
ygraph (http://www.aei.mpg.de/~pollney/ygraph/) may also be able to directly plot the BH_diagnostics
files.
Given a horizon-shape data file h.t105.h4.gp, the gnuplot command
splot ’h.t105.h4.gp’ with lines
will plot the \(h(\text {angle})\) function, with the \(x\) and \(y\) axes of the plot being the two “unwrapped” angular coordinates on \(S^2\), in
degrees, and the \(z\) axis being \(h(\text {angle})\). However, in practice this usually isn’t very informative. Instead, you probably
want the gnuplot command
splot ’h.t105.h4.gp’ using 4:5:6 with lines
which will plot the 3-D shape of the apparent horizon surface.
The src/misc directory of the AHFinderDirect source code contains several perl scripts which are
useful in visualizing AHFinderDirect output. In particular, the script select.plane selects a
particular 2-D plane. If you put this in your Unix path, it can be used with a gnuplot command
like
splot ’<select.plane xy <h.t105.h4.gp’ using 4:5 with lines
to show the shape of an apparent horizon in the xy
plane.
Another Visualization option is OpenDX (http://www.opendx.org/). Thomas Radke’s has written some
OpenDX macros ImportAHFinderDirectGnuplot.net and ImportAHFinderDirectGnuplotPatch.net
to import AHFinderDirect horizon-shape data files. These macros use a set of “control files”
named *.dx, one per horizon, which AHFinderDirect (by default) writes into the same directory
as the main horizon–shape output files. You can get these macros by anonymous CVS with the
command
cvs -d :pserver:cvs_anon@cvs.aei.mpg.de:/numrelcvs \
checkout AEIPhysics/Visualization/OpenDX
Another Visualization option is to produce files in the standard Xdmf [?] file format which can be visualized for
example using VisIt [?]. Frank Löffler has written a python script AH2xdmf.py, which is included in this
thorn’s code repository, which generates such files from AHFinderDirect’s output from horizon shape files
h.t%d.ah%d.gp\. Please see its help text for details.
7 Accuracy
The apparent horizon positions are typically computed very accurately; tests on Kerr spacetimes give typical
errors of \(10^{-4}m\) to \(10^{-5}m\).
The various diagnostics printed to standard output and written to the black hole diagnostics file(s), are typically
computed to accuracies on the order of a part per million or so.
Note, however, that the irreducible mass \(m_{\text {e}}\) may differ considerably from the black hole’s local mass or its
contribution to the slice’s ADM mass. For example, for Kerr spacetime in Kerr-Schild coordinates, \(m_{\text {e}}/m_{\text {M}} = 0.949\), \(0.894\), and \(0.723\) for
spin parameters \(a \equiv J/m^2 = 0.6\), \(0.8\), and \(0.999\), respectively. It would be better to (also) use the “isolated horizons” formalism of [?]; at
some point this thorn may be enhanced to do this.
8 Examples
There are a few example parameter files in the par/ directory, including Kerr initial data, Misner initial data,
and Misner time-evolution tests. The Kerr-tiny.par parameter file is close to a minimal AHFinderDirect
example:
# This parameter file sets up Kerr/Kerr-Schild initial data, then
# finds the apparent horizon in it. The local coordinate system origin
# and the initial guess are both deliberately de-centered with respect
# to the black hole, to make this a non-trivial test for the apparent
# horizon finder.
#
# This parameter file is "tiny" in the sense that it sets only a
# small number of AHFinderDirect parameters.
# flesh
cactus::cctk_itlast = 0
ActiveThorns = "PUGH"
driver::ghost_size = 2
driver::global_nx = 31
driver::global_ny = 31
driver::global_nz = 19
ActiveThorns = "CoordBase CartGrid3D"
grid::domain = "bitant"
grid::avoid_origin = false
grid::type = "byspacing"
grid::dxyz = 0.2
ActiveThorns = "ADMBase ADMCoupling StaticConformal Spacemask CoordGauge Exact"
ADMBase::initial_lapse = "exact"
ADMBase::initial_shift = "exact"
ADMBase::initial_data = "exact"
ADMBase::lapse_evolution_method = "static"
ADMBase::shift_evolution_method = "static"
ADMBase::metric_type = "physical"
Exact::exact_model = "Kerr/Kerr-Schild"
Exact::Kerr_KerrSchild__mass = 1.0
Exact::Kerr_KerrSchild__spin = 0.6
########################################
ActiveThorns = "IOUtil"
IOUtil::parfile_write = "no"
########################################
ActiveThorns = "SphericalSurface"
ActiveThorns = "AEILocalInterp PUGHInterp PUGHReduce AHFinderDirect"
AHFinderDirect::h_base_file_name = "Kerr-tiny.h"
AHFinderDirect::N_horizons = 1
AHFinderDirect::origin_x[1] = 0.5
AHFinderDirect::origin_y[1] = 0.7
AHFinderDirect::origin_z[1] = 0.0
AHFinderDirect::initial_guess_method[1] = "coordinate sphere"
AHFinderDirect::initial_guess__coord_sphere__x_center[1] = -0.2
AHFinderDirect::initial_guess__coord_sphere__y_center[1] = 0.3
AHFinderDirect::initial_guess__coord_sphere__z_center[1] = 0.0
AHFinderDirect::initial_guess__coord_sphere__radius[1] = 2.0
9 Surfaces of Constant Expansion
Surfaces of Constant Expansion (CE surfaces) are introduced in [?] as a generalisation of apparent horizons
(AH). On an AH surface, the expansion is zero everywhere. On a CE surfaces, the expansion is still everywhere
the same, but it need not be zero. CE surfaces are also a generalisation of Constant Mean Curvature surfaces
(CMC surfaces); both are identical when the extrinsic curvature vanishes. As described in [?], it is likely that CE
surfaces foliate the spacelike hypersurface outside of some interior region. This interior region is inside the
common apparent horizon, if it exists.
CE surfaces can give some insight into the spacetime, because they can be used to analyse the part of the
spacelike hypersurface “between the horizons and infinity”. Most notably, they can be used to look at the region
where a common horizon is about to (or believed to) form. Similarly, one can use them for collapsing stars where
an apparent horizon has not yet formed.
10 Pretracking
Apparent horizon pretracking is introduced in [?]. This is an application of CE surfaces. Even when there is no
common horizon, there are still common CE surfaces surrounding multiple black holes. Pretracking consists of
tracking in time the smallest common CE surface that can be found. It is reasonable to believe that this surface
will evolve into the common horizon at the time where this common horizon begins to exist. The expansion of
this smallest CE surface is also an indication of how close the spacelike hypersurface is to having a common
apparent horizon.
11 How AHFinderDirect Works
AHFinderDirect uses the apparent horizon (henceforth “horizon”) finding algorithm of [?], modified slightly to
work with \(g_\ij \) and \(K_\ij \) on a Cartesian (\(xyz\)) grid. The algorithm is described in detail in [?].
11.1 General Description of the Algorithm
As described above, I parameterizes the horizon shape by \(r = h(\text {angle})\) for some single-value function \(h: S^2 \to \Re ^+\). The apparent
horizon equation \((\ref {AHFinderDirect/eqn-horizon})\) then becomes a 2-D elliptic PDE on \(S^2\) for the function \(h\). I finite difference this in
angle to obtain a system of simultaneous nonlinear algebraic equations for \(h\) at the angular grid
points, and solve this system of equations by a global Newton’s method (or a variant with improved
convergence).
Computationally, this algorithm has 3 main parts:
-
Computation of the “horizon function” \(\Theta (h)\) given a trial surface defined by a trial horizon shape function
\(h\). This is done by interpolating the Cactus geometry fields \(g_\ij \) and \(K_\ij \) (and optionally \(\psi \)) from the 3-D
\(xyz\) grid to the (2-D set of) trial-horizon-surface grid points (also computing \(\partial _k g_\ij \) in the interpolation
process), then doing all further computations with angular grid functions defined solely on \(S^2\) (i.e. at
the horizon-surface grid points).
-
Computation of the Jacobian matrix \(\Jac [\Theta (h)]\) of \(\Theta (h)\). This thorn incorporates the “symbolic differentiation”
technique described in [?], so this computation is quite fast. The Jacobian is a highly sparse matrix;
AHFinderDirect has code to store it as either a dense matrix (for debugging purposes), or a
sparse matrix (the default). Which option is used is determined by a compile-time configuration in
src/include/config.h.
-
Solving the nonlinear equations \(\Theta (h) = 0\) by a global Newton’s method or a variant. How this is done depends on
how the Jacobian is stored. At present,
-
If AHFinderDirect is configured to store the Jacobian as a dense matrix, then LAPACK is
used to solve the linear equations.
-
If AHFinderDirect is configured to store the Jacobian as a sparse matrix, then an
incomplete-\(\sf LU\)-decomposition–conjugate-gradient solver is used.
By default only the sparse-matrix code is configured, so LAPACK isn’t used and there’s no need to link
with the LAPACK library.
11.2 The Multipatch System
Perhaps the most unusual feature of AHFinderDirect is the “multipatch” system used to cover \(S^2\) without
coordinate singularities. In general there are 6 patches, one each covering a neighborhood of the \(\pm z\), \(\pm x\), and \(\pm y\)
axes, but this may be reduced in the presence of suitable symmetries. For example, figure 2 on
page 39 shows a system of 3 patches covering the \(+xyz\) octant of \(S^2\). This would be suitable for finding an
apparent horizon with mirror symmetry about the (local) \(z=0\) plane, and either 90 degree periodic
rotation symmetry about the (local) \(z\) axis, or mirror symmetry about each of the (local) \(x\) and
\(y\) axes.
To allow easy angular finite differencing within the patch system, each patch is extended beyond its nominal extent by a
“ghost zone”
(2 grid points wide in figure 2). Angular grid function values in the ghost zone can be obtained by interpatch
interpolation
or by applying symmetry operations. Once this is done, then angular finite differencing within the nominal
extent of each patch can proceed normally, ignoring the patch boundaries. AHFinderDirect can be
configured at compile time to use either 2nd order or 4th order angular finite differencing (3 point or
5 point angular molecules); the default is 4th order (5 point). This is configured at compile time in
src/include/config.h.
By default AHFinderDirect will automagically choose a patch system type for each apparent
horizon searched for, based on the local coordinate origin and the symmetries implicit in the Cactus
grid type. This generally works well, but if desired you can instead manually specify the patch
system type, the angular resolution, the width of the ghost zones, etc. See the param.ccl file for
details.
11.3 Other Software Used
AHFinderDirect’s src/sparse-matrix/ directory contains various sparse-matrix libraries, which have their
own copyrights and licensing terms:
The src/sparse-matrix/umfpack/ directory contains a subset of the files in UMFPACK version 4.0
(11.Apr.2002). This code is copyright (©) 2002 by Timothy A. Davis, and is subect to the UMFPACK
License:
Your use or distribution of UMFPACK or any modified version of
UMFPACK implies that you agree to this License.
THIS MATERIAL IS PROVIDED AS IS, WITH ABSOLUTELY NO WARRANTY
EXPRESSED OR IMPLIED. ANY USE IS AT YOUR OWN RISK.
Permission is hereby granted to use or copy this program, provided
that the Copyright, this License, and the Availability of the original
version is retained on all copies. User documentation of any code that
uses UMFPACK or any modified version of UMFPACK code must cite the
Copyright, this License, the Availability note, and "Used by permission."
Permission to modify the code and to distribute modified code is granted,
provided the Copyright, this License, and the Availability note are
retained, and a notice that the code was modified is included. This
software was developed with support from the National Science Foundation,
and is provided to you free of charge.
12 Other Related Thorns
If you’re interested in AHFinderDirect, you might also be interested in some other related thorns:
-
EHFinder
-
(in the AEIDevelopment arrangement) was written by Peter Diener, and finds the event
horizon(s) in a numerically computed spacetime. It’s described in detail in the paper [?].
-
AHFinder
-
(in the CactusEinstein arrangement) was written by Miguel Alcubierre, and includes two different
algorithms for finding apparent horizons, a minimization method and a “fast flow” method based
on [?]. Unfortunately, both methods are very slow in practice.
-
TGRapparentHorizon2D
-
(in the TAT arrangement) was written by Erik Schnetter, and is another apparent horizon finder.
It uses methods very similar to this thorn, and (like this thorn) is very fast and accurate. However,
it’s no longer under active development. It’s described in detail in the papers [?] and [?].
-
AHFinderDirect (Erik branch)
-
(in the AEIThorns arrangement)
Erik Schnetter has added a number of new features to AHFinderDirect on a CVS branch with
the tag Erik, including horizon pretracking (to locate places where horizons are about to form), and
the ability to find constant-expansion and constant-mean-curvature surfaces specified by their areal
radius. We hope to integrate these into the main AHFinderDirect branch during the summer of
2004.
13 Acknowledgments
I thank Peter Diener, Ian Hawke, and Erik Schnetter for many valuable conversations. I think Thomas Radke for
his work on the new interpolators. I thank the whole Cactus crew for a great infrastructure!
Erik Schnetter originally implemented a number of improvements to this thorn, notably the SphericalSurface
interface and the new features in the Erik branch.
I thank the Alexander von Humboldt foundation and the AEI visitors’ and postdoctoral fellowships programs for
financial support.
14 Parameters
|
|
|
| ascii_gnuplot_file_name_extension | Scope: private | STRING |
|
|
|
| Description: extension for ASCII (gnuplot) data files
|
|
|
|
| Range | | Default: gp |
| .+ | any nonempty string
|
|
|
|
| |
|
|
|
| bh_diagnostics_base_file_name | Scope: private | STRING |
|
|
|
| Description: base file name for BH diagnostics output file(s)
|
|
|
|
| Range | | Default: BH_diagnostics |
| .+ | any nonempty string
|
|
|
|
| |
|
|
|
| bh_diagnostics_directory | Scope: private | STRING |
|
|
|
| Description: directory for BH diagnostics output file(s)
|
|
|
|
| Range | | Default: (none) |
| .+ | any nonempty string
|
| | an empty string to default to IO::out_dir
|
|
|
|
| |
|
|
|
| bh_diagnostics_file_name_extension | Scope: private | STRING |
|
|
|
| Description: extension for BH diagnostics data files
|
|
|
|
| Range | | Default: gp |
| .+ | any nonempty string
|
|
|
|
| |
|
|
|
| check_that_geometry_is_finite | Scope: private | BOOLEAN |
|
|
|
| Description: should we check the interpolated geometry variables are finite?
|
|
|
|
| | | Default: true |
|
|
|
| |
|
|
|
| check_that_h_is_finite | Scope: private | BOOLEAN |
|
|
|
| Description: should we check that horizon shape function h is finite?
|
|
|
|
| | | Default: true |
|
|
|
| |
|
|
|
| coordinate_system_name | Scope: private | STRING |
|
|
|
| Description: name under which the coordinate system is registered in Cactus
|
|
|
|
| Range | | Default: cart3d |
| .+ | any nonempty string
|
|
|
|
| |
|
|
|
| debugging_output_at_each_newton_iteration | Scope: private | BOOLEAN |
|
|
|
| Description: should we output {h, Theta, delta_h}at each Newton iteration?
|
|
|
|
| | | Default: false |
|
|
|
| |
|
|
|
| delta_h_base_file_name | Scope: private | STRING |
|
|
|
| Description: base file name for horizon-shape-update Delta_h output file(s)
|
|
|
|
| Range | | Default: Delta_h |
| .+ | any nonempty string
|
|
|
|
| |
|
|
|
| depends_on | Scope: private | INT |
|
|
|
| Description: the other horizon that this horizon depends on
|
|
|
|
| Range | | Default: (none) |
| | the horizon is independent
|
| 1:100 | horizon index
|
|
|
|
| |
|
|
|
| desired_value | Scope: private | REAL |
|
|
|
| Description: search for a surface with this (constant) value
|
|
|
|
| Range | | Default: 0.0 |
| *:* | any real number
|
|
|
|
| |
|
|
|
| desired_value_factor | Scope: private | REAL |
|
|
|
| Description: factor between this horizon’s and the other horizon’s desired value, applied before
the offset
|
|
|
|
| Range | | Default: 1.0 |
| *:* |
|
|
|
|
| |
|
|
|
| desired_value_offset | Scope: private | REAL |
|
|
|
| Description: difference between this horizon’s and the other horizon’s desired value, applied after
the factor
|
|
|
|
| Range | | Default: 0.0 |
| *:* |
|
|
|
|
| |
|
|
|
| disable_horizon | Scope: private | BOOLEAN |
|
|
|
| Description: should this horizon be disabled?
|
|
|
|
| | | Default: false |
|
|
|
| |
|
|
|
| dont_find_after_individual | Scope: private | INT |
|
|
|
| Description: when should we stop finding individual apparent horizons?
|
|
|
|
| Range | | Default: -1 |
| 0:* | after this iteration (exclusively)
|
| -1 | do not use this parameter
|
|
|
|
| |
|
|
|
| dont_find_after_individual_time | Scope: private | REAL |
|
|
|
| Description: when should we stop finding individual apparent horizons?
|
|
|
|
| Range | | Default: 0.0 |
| *:*
| ”after this time (exclusively); ignore this value if it is less
than or equal to find_after_individua l_time”
|
|
|
|
| |
|
|
|
| find_after_individual | Scope: private | INT |
|
|
|
| Description: when should we start to find individual apparent horizons?
|
|
|
|
| Range | | Default: (none) |
| 0:* | after this iteration (inclusively)
|
|
|
|
| |
|
|
|
| find_after_individual_time | Scope: private | REAL |
|
|
|
| Description: when should we start to find individual apparent horizons?
|
|
|
|
| Range | | Default: 0.0 |
| *:* | after this time (inclusively)
|
|
|
|
| |
|
|
|
| find_every | Scope: private | INT |
|
|
|
| Description: how often should we try to find apparent horizons?
|
|
|
|
| Range | | Default: 1 |
| | don’t find AHs at all (this thorn is a no-op)
|
| 1:* | any integer >= 1
|
|
|
|
| |
|
|
|
| find_every_individual | Scope: private | INT |
|
|
|
| Description: how often should we try to find individual apparent horizons? (overrides find_every)
|
|
|
|
| Range | | Default: -1 |
| -1 | use the value of find_every
|
| | don’t find this AH at all
|
| 1:* | any integer >= 1
|
|
|
|
| |
|
|
|
| geometry__schwarzschild_ef__delta_xyz | Scope: private | REAL |
|
|
|
| Description: finite diff pseuo-grid spacing for computing partial_k g_ij
|
|
|
|
| Range | | Default: 1.0e-6 |
| (0.0:* | any real number > 0
|
|
|
|
| |
|
|
|
| geometry__schwarzschild_ef__epsilon | Scope: private | REAL |
|
|
|
Description: threshold for sin theta = (x theta = (x +y +y )/r )/r below which we use z axis limits below which we use z axis limits
|
|
|
|
| Range | | Default: 1.0e-9 |
| (0.0:*
| this should be somewhat above the floating-point
roundoff level
|
|
|
|
| |
|
|
|
| geometry__schwarzschild_ef__mass | Scope: private | REAL |
|
|
|
| Description: mass of Schwarzschild BH
|
|
|
|
| Range | | Default: 1.0 |
| (0.0:* | BH mass = any real number > 0
|
|
|
|
| |
|
|
|
| geometry__schwarzschild_ef__x_posn | Scope: private | REAL |
|
|
|
| Description: x coordinate of Schwarzschild BH
|
|
|
|
| Range | | Default: 0.0 |
| *:* | any real number
|
|
|
|
| |
|
|
|
| geometry__schwarzschild_ef__y_posn | Scope: private | REAL |
|
|
|
| Description: y coordinate of Schwarzschild BH
|
|
|
|
| Range | | Default: 0.0 |
| *:* | any real number
|
|
|
|
| |
|
|
|
| geometry__schwarzschild_ef__z_posn | Scope: private | REAL |
|
|
|
| Description: z coordinate of Schwarzschild BH
|
|
|
|
| Range | | Default: 0.0 |
| *:* | any real number
|
|
|
|
| |
|
|
|
| geometry_interpolator_name | Scope: private | STRING |
|
|
|
| Description: name under which the geometry interpolation operator is registered in Cactus
|
|
|
|
| Range | | Default: Hermite polynomial interpolation |
| .+ | any nonempty string
|
|
|
|
| |
|
|
|
| geometry_interpolator_pars | Scope: private | STRING |
|
|
|
| Description: parameters for the geometry interpolator
|
|
|
|
| Range | | Default: order=2 boundary_off_centering_tolerance={1.0e-10 1.0e-10 1.0e-10 1.0e-10 1.0e-10 1.0e-10} boundary_extrapolation_tolerance={0.0 0.0 0.0 0.0 0.0 0.0} |
| .*
| ”any string acceptable to Util_TableSetFromStr ing()
and to the interpolator”
|
|
|
|
| |
|
|
|
| ghost_zone_width | Scope: private | INT |
|
|
|
| Description: number of ghost zones on each side of a patch
|
|
|
|
| Range | | Default: 2 |
| 0:* | any integer >= 0
|
|
|
|
| |
|
|
|
| h_base_file_name | Scope: private | STRING |
|
|
|
| Description: base file name for horizon shape h input/output file(s)
|
|
|
|
| Range | | Default: h |
| .+ | any nonempty string
|
|
|
|
| |
|
|
|
| h_directory | Scope: private | STRING |
|
|
|
| Description: directory for horizon shape and other similar output (or input) file(s)
|
|
|
|
| Range | | Default: (none) |
| .+ | any nonempty string
|
| | an empty string to default to IO::out_dir
|
|
|
|
| |
|
|
|
| h_min_digits | Scope: private | INT |
|
|
|
| Description: minimum number of digits for the iteration number in the file name
|
|
|
|
| Range | | Default: (none) |
| 0:* |
|
|
|
|
| |
|
|
|
| hardwire_schwarzschild_ef_geometry | Scope: private | BOOLEAN |
|
|
|
| Description: should we hard-wire the geometry to Schwarzschild/EF instead of interpolating from
the Cactus grid?
|
|
|
|
| | | Default: false |
|
|
|
| |
|
|
|
| hdf5_file_name_extension | Scope: private | STRING |
|
|
|
| Description: extension for HDF5 data files
|
|
|
|
| Range | | Default: h5 |
| .+ | any nonempty string
|
|
|
|
| |
|
|
|
| ilucg__error_tolerance | Scope: private | REAL |
|
|
|
| Description: error tolerance for conjugate gradient iteration
|
|
|
|
| Range | | Default: 1.0e-10 |
| (*:0.0)
| negative ==> scale the absolute value by the floating
point roundoff threshold, e.g. -256.0 means to allow the
last 8 bits of the solution to be in error
|
| (0.0:*) | positive ==> error tolerance
|
|
|
|
| |
|
|
|
| ilucg__limit_cg_iterations | Scope: private | BOOLEAN |
|
|
|
| Description: should we limit the maximum number of conjugate gradient iterations allowed?
|
|
|
|
| Range | | Default: true |
| false | no limit on CG iterations
|
| true | limit to Neqns CG iterations
|
|
|
|
| |
|
|
|
| initial_guess__coord_ellipsoid__x_center | Scope: private | REAL |
|
|
|
| Description: x coordinate of ellipsoid center
|
|
|
|
| Range | | Default: 0.0 |
| *:* | any real number
|
|
|
|
| |
|
|
|
| initial_guess__coord_ellipsoid__x_radius | Scope: private | REAL |
|
|
|
| Description: x radius of ellipsoid
|
|
|
|
| Range | | Default: 2.0 |
| (0.0:* | any real number > 0.0
|
|
|
|
| |
|
|
|
| initial_guess__coord_ellipsoid__y_center | Scope: private | REAL |
|
|
|
| Description: y coordinate of ellipsoid center
|
|
|
|
| Range | | Default: 0.0 |
| *:* | any real number
|
|
|
|
| |
|
|
|
| initial_guess__coord_ellipsoid__y_radius | Scope: private | REAL |
|
|
|
| Description: y radius of ellipsoid
|
|
|
|
| Range | | Default: 2.0 |
| (0.0:* | any real number > 0.0
|
|
|
|
| |
|
|
|
| initial_guess__coord_ellipsoid__z_center | Scope: private | REAL |
|
|
|
| Description: z coordinate of ellipsoid center
|
|
|
|
| Range | | Default: 0.0 |
| *:* | any real number
|
|
|
|
| |
|
|
|
| initial_guess__coord_ellipsoid__z_radius | Scope: private | REAL |
|
|
|
| Description: z radius of ellipsoid
|
|
|
|
| Range | | Default: 2.0 |
| (0.0:* | any real number > 0.0
|
|
|
|
| |
|
|
|
| initial_guess__coord_sphere__radius | Scope: private | REAL |
|
|
|
| Description: radius of sphere
|
|
|
|
| Range | | Default: 2.0 |
| (0.0:* | any real number > 0.0
|
|
|
|
| |
|
|
|
| initial_guess__coord_sphere__x_center | Scope: private | REAL |
|
|
|
| Description: x coordinate of sphere center
|
|
|
|
| Range | | Default: 0.0 |
| *:* | any real number
|
|
|
|
| |
|
|
|
| initial_guess__coord_sphere__y_center | Scope: private | REAL |
|
|
|
| Description: y coordinate of sphere center
|
|
|
|
| Range | | Default: 0.0 |
| *:* | any real number
|
|
|
|
| |
|
|
|
| initial_guess__coord_sphere__z_center | Scope: private | REAL |
|
|
|
| Description: z coordinate of sphere center
|
|
|
|
| Range | | Default: 0.0 |
| *:* | any real number
|
|
|
|
| |
|
|
|
| initial_guess__kerr_kerr__mass | Scope: private | REAL |
|
|
|
| Description: mass of Kerr BH
|
|
|
|
| Range | | Default: 1.0 |
| (0.0:* | BH mass = any real number > 0
|
|
|
|
| |
|
|
|
| initial_guess__kerr_kerr__spin | Scope: private | REAL |
|
|
|
Description: dimensionless spin a=J/m of Kerr BH of Kerr BH
|
|
|
|
| Range | | Default: 0.6 |
| (-1.0:1.0)
| dimensionless BH spin = J/m  = any real number with
absolute value < 1 |
|
|
|
| |
|
|
|
| initial_guess__kerr_kerr__x_posn | Scope: private | REAL |
|
|
|
| Description: x coordinate of Kerr BH
|
|
|
|
| Range | | Default: 0.0 |
| *:* | any real number
|
|
|
|
| |
|
|
|
| initial_guess__kerr_kerr__y_posn | Scope: private | REAL |
|
|
|
| Description: y coordinate of Kerr BH
|
|
|
|
| Range | | Default: 0.0 |
| *:* | any real number
|
|
|
|
| |
|
|
|
| initial_guess__kerr_kerr__z_posn | Scope: private | REAL |
|
|
|
| Description: z coordinate of Kerr BH
|
|
|
|
| Range | | Default: 0.0 |
| *:* | any real number
|
|
|
|
| |
|
|
|
| initial_guess__kerr_kerrschild__mass | Scope: private | REAL |
|
|
|
| Description: mass of Kerr BH
|
|
|
|
| Range | | Default: 1.0 |
| (0.0:* | BH mass = any real number > 0
|
|
|
|
| |
|
|
|
| initial_guess__kerr_kerrschild__spin | Scope: private | REAL |
|
|
|
Description: dimensionless spin a=J/m of Kerr BH of Kerr BH
|
|
|
|
| Range | | Default: 0.6 |
| (-1.0:1.0)
| dimensionless BH spin = J/m  = any real number with
absolute value < 1 |
|
|
|
| |
|
|
|
| initial_guess__kerr_kerrschild__x_posn | Scope: private | REAL |
|
|
|
| Description: x coordinate of Kerr BH
|
|
|
|
| Range | | Default: 0.0 |
| *:* | any real number
|
|
|
|
| |
|
|
|
| initial_guess__kerr_kerrschild__y_posn | Scope: private | REAL |
|
|
|
| Description: y coordinate of Kerr BH
|
|
|
|
| Range | | Default: 0.0 |
| *:* | any real number
|
|
|
|
| |
|
|
|
| initial_guess__kerr_kerrschild__z_posn | Scope: private | REAL |
|
|
|
| Description: z coordinate of Kerr BH
|
|
|
|
| Range | | Default: 0.0 |
| *:* | any real number
|
|
|
|
| |
|
|
|
| initial_guess__read_from_named_file__file_name | Scope: private | STRING |
|
|
|
| Description: file name to read initial guess from
|
|
|
|
| Range | | Default: h.gp |
| .+ | file name to read initial guess from
|
|
|
|
| |
|
|
|
| initial_guess_method | Scope: private | KEYWORD |
|
|
|
| Description: method used to set up initial guess for apparent horizon shape
|
|
|
|
| Range | | Default: coordinate sphere |
| read from named file | read from explicitly-named input file
|
| read from h file
| read from input file named the same as the (later) h
output file
|
| Kerr/Kerr
| set to the (analytical) horizon of Kerr spacetime in Kerr
coordinates (n.b. Schwarzschild/EF is the special case
spin=0 of this)
|
| Kerr/Kerr-Schild
| set to the (analytical) horizon of Kerr spacetime in
Kerr-Schild coordinates
|
| coordinate sphere | set to a coordinate sphere
|
| coordinate ellipsoid | set to a coordinate ellipsoid
|
|
|
|
| |
|
|
|
| integral_method | Scope: private | KEYWORD |
|
|
|
| Description: how do we compute integrals over the horizon?
|
|
|
|
| Range | | Default: automatic choice |
| trapezoid | alternate name for trapezoid rule
|
| trapezoid rule | trapezoid rule (2nd order for smooth functions)
|
| Simpson | alternate name for Simpson’s rule
|
| Simpson’s rule
| Simpson’s rule (4th order for smooth fns, requires N to
be even)
|
| Simpson (variant) | alternate name for Simpson’s rule variant
|
| see [1] below
| Simpson’s rule variant (4th order for smooth fns, requires
N >= 7)
|
| automatic choice
| choose Simpson’s rule or variant if applicable, otherwise
trapezoid rule
|
|
|
|
| |
[1]
Simpson’s rule (variant)
|
|
|
| interpatch_interpolator_name | Scope: private | STRING |
|
|
|
| Description: name under which the interpatch interpolation operator is registered in Cactus
|
|
|
|
| Range | | Default: Lagrange polynomial interpolation |
| .+ | any string (in practice it should be nonempty)
|
|
|
|
| |
|
|
|
| interpatch_interpolator_pars | Scope: private | STRING |
|
|
|
| Description: parameters for the interpatch interpolator
|
|
|
|
| Range | | Default: order=5 |
| .*
| ”any string acceptable to Util_TableSetFromStr ing()
and to the interpolator”
|
|
|
|
| |
|
|
|
| jacobian_base_file_name | Scope: private | STRING |
|
|
|
| Description: base file name for Jacobian output file(s)
|
|
|
|
| Range | | Default: Jacobian.dat |
| .+ | any valid file name
|
|
|
|
| |
|
|
|
| jacobian_compute_method | Scope: private | KEYWORD |
|
|
|
| Description: how do we compute the Jacobian matrix?
|
|
|
|
| Range | | Default: symbolic differentiation with finite diff d/dr |
| see [1] below | n.b. this is *very* slow
|
| see [1] below | fast, tricky programming, uses only gij, dx gij, Kij
|
| see [1] below
| fast, tricky programming, uses gij, dx gij, dxx gij, Kij, dx
Kij
|
|
|
|
| |
[1]
numerical perturbation
[1]
symbolic differentiation with finite diff d/dr
[1]
symbolic differentiation
|
|
|
| jacobian_perturbation_amplitude | Scope: private | REAL |
|
|
|
| Description: perturbation amplitude for 1-sided finite differencing for Jacobians
|
|
|
|
| Range | | Default: 1.0e-6 |
| (0.0:* | any real number > 0
|
|
|
|
| |
|
|
|
| jacobian_store_solve_method | Scope: private | KEYWORD |
|
|
|
| Description: how do we store/linear-solve the Jacobian matrix?
|
|
|
|
| Range | | Default: row-oriented sparse matrix/UMFPACK |
| dense matrix/LAPACK
| store as (Fortran) dense matrix, solve with LAPACK
routines
|
| see [1] below
| store as sparse matrix (row-oriented storage format),
solve with ILUCG (incomplete LU decomposition -
conjugate gradient) method
|
| see [1] below
| store as sparse matrix (row-oriented storage format),
solve with UMFPACK (sparse LU decomposition)
method
|
|
|
|
| |
[1]
row-oriented sparse matrix/ILUCG
[1]
row-oriented sparse matrix/UMFPACK
|
|
|
| mask_buffer_thickness | Scope: private | REAL |
|
|
|
| Description: thickness (in Cactus base grid spacings) of the ’buffer’ mask region
|
|
|
|
| Range | | Default: 5.0 |
| *:* | any real number; typically this will be positive
|
|
|
|
| |
|
|
|
| mask_is_noshrink | Scope: private | BOOLEAN |
|
|
|
| Description: should we prevent the inside & buffer regions from ever shrinking?
|
|
|
|
| | | Default: true |
|
|
|
| |
|
|
|
| mask_radius_multiplier | Scope: private | REAL |
|
|
|
| Description: radius multiplier to define the ’inside’ mask region
|
|
|
|
| Range | | Default: 0.8 |
| (0:*)
| any positive real number; typically this will be slightly
less than 1.0
|
|
|
|
| |
|
|
|
| mask_radius_offset | Scope: private | REAL |
|
|
|
| Description: radius offset (in Cactus base grid spacings) to define the ’inside’ mask region
|
|
|
|
| Range | | Default: -5.0 |
| *:* | any real number; typically this will be negative
|
|
|
|
| |
|
|
|
| max_allowable_delta_h_over_h | Scope: private | REAL |
|
|
|
| Description: don’t let horizon move > this fraction of mean radius in a Newton iteration
|
|
|
|
| Range | | Default: 0.1 |
| (0.0:* | any positive real number
|
|
|
|
| |
|
|
|
| max_allowable_horizon_radius | Scope: private | REAL |
|
|
|
| Description: max mean-coordinate-radius allowed for any trial surface before we give up and say
we can’t find this horizon
|
|
|
|
| Range | | Default: 1.0e10 |
| (0.0:* | any positive real number
|
|
|
|
| |
|
|
|
| max_allowable_theta | Scope: private | REAL |
|
|
|
| Description: max ——Theta——_infinity allowed for any trial surface before we give up and say
we can’t find this horizon
|
|
|
|
| Range | | Default: 1.0e10 |
| (0.0:* | any positive real number
|
|
|
|
| |
|
|
|
| max_allowable_theta_growth_iterations | Scope: private | INT |
|
|
|
| Description: max number of consecutive iterations during which ——Theta——_infinity is
allowed to grow before we give up and say we can’t find this horizon
|
|
|
|
| Range | | Default: (none) |
| | infinitly many
|
| 1:* | that many
|
|
|
|
| |
|
|
|
| max_allowable_theta_nonshrink_iterations | Scope: private | INT |
|
|
|
| Description: max number of consecutive iterations during which ——Theta——_infinity is
allowed to oscillate without shrinking before we give up and say we can’t find this horizon
|
|
|
|
| Range | | Default: (none) |
| | infinitly many
|
| 1:* | that many
|
|
|
|
| |
|
|
|
| max_n_zones_per_right_angle | Scope: private | INT |
|
|
|
| Description: the maximum of all N_zones_per_right_angle
|
|
|
|
| Range | | Default: 18 |
| 1:*
| ”must be at least the maximum of all
N_zones_per_right_an gle”
|
|
|
|
| |
|
|
|
| max_newton_iterations__initial | Scope: private | INT |
|
|
|
| Description: maximum number of Newton iterations before giving up when initially finding a
given horizon
|
|
|
|
| Range | | Default: 20 |
| (0:* | any positive integer
|
|
|
|
| |
|
|
|
| max_newton_iterations__subsequent | Scope: private | INT |
|
|
|
| Description: maximum number of Newton iterations before giving up when re-finding a given
horizon after finding it before
|
|
|
|
| Range | | Default: 10 |
| (0:* | any positive integer
|
|
|
|
| |
|
|
|
| mean_curvature_base_file_name | Scope: private | STRING |
|
|
|
| Description: base file name for mean_curvature(h) output file(s)
|
|
|
|
| Range | | Default: mean_curvature |
| .+ | any nonempty string
|
|
|
|
| |
|
|
|
| method | Scope: private | KEYWORD |
|
|
|
| Description: what should this thorn do for each apparent horizon?
|
|
|
|
| Range | | Default: find horizons |
| evaluate expansions | evaluate the LHS function Theta(h)
|
| see [1] below
| ”compute/print horizon 1’s J[Theta(h)] Jacobian matrix
(possibly in multiple ways, depending on the
test_all_Jacobian_me thods parameter)”
|
| find horizons | find the apparent horizon
|
|
|
|
| |
[1]
test expansion Jacobians
|
|
|
| min_horizon_radius_points_for_mask | Scope: private | REAL |
|
|
|
| Description: only set mask if min r_inner >= this number of local grid spacings
|
|
|
|
| Range | | Default: -1.0e10 |
| *:* | any real number
|
|
|
|
| |
|
|
|
| move_origins | Scope: private | BOOLEAN |
|
|
|
| Description: move the origins with the horizons
|
|
|
|
| | | Default: no |
|
|
|
| |
|
|
|
| n_horizons | Scope: private | INT |
|
|
|
| Description: number of apparent horizons to search for
|
|
|
|
| Range | | Default: 1 |
| | turn this thorn into a fancy no-op :)
|
| 1:100 | search for this many apparent horizons
|
|
|
|
| |
|
|
|
| n_zones_per_right_angle | Scope: private | INT |
|
|
|
| Description: sets angular resolution of patch systems
|
|
|
|
| Range | | Default: 18 |
| 1:*
| any integer >= 1; must be even for patch systems other
than full-sphere
|
|
|
|
| |
|
|
|
| new_style_mask_bitfield_name | Scope: private | STRING |
|
|
|
| Description: name of the new-style mask bit field (’type’) as registered with SpaceMask
|
|
|
|
| Range | | Default: mask |
| .+
| any valid bit field (’type’) name registered with the
SpaceMask thorn
|
|
|
|
| |
|
|
|
| new_style_mask_buffer_value | Scope: private | STRING |
|
|
|
| Description: set the specified bit field of the new-style mask to this named state at grid points in
the ’buffer’ region
|
|
|
|
| Range | | Default: buffer |
| .+ | any state name registered with the SpaceMask thorn
|
|
|
|
| |
|
|
|
| new_style_mask_gridfn_name | Scope: private | STRING |
|
|
|
| Description: name of the new-style mask grid function
|
|
|
|
| Range | | Default: SpaceMask::space_mask |
| .+ | any valid Cactus grid function name
|
|
|
|
| |
|
|
|
| new_style_mask_inside_value | Scope: private | STRING |
|
|
|
| Description: set the specified bit field of the new-style mask to this named state at grid points in
the ’inside’ region
|
|
|
|
| Range | | Default: inside |
| .+ | any state name registered with the SpaceMask thorn
|
|
|
|
| |
|
|
|
| new_style_mask_outside_value | Scope: private | STRING |
|
|
|
| Description: set the specified bit field of the new-style mask to this named state at grid points in
the ’outside’ region
|
|
|
|
| Range | | Default: outside |
| .+ | any state name registered with the SpaceMask thorn
|
|
|
|
| |
|
|
|
| old_style_mask_buffer_value | Scope: private | REAL |
|
|
|
| Description: set the old-style mask to this value in the ’buffer’ region
|
|
|
|
| Range | | Default: 0.5 |
| *:* | any real number
|
|
|
|
| |
|
|
|
| old_style_mask_gridfn_name | Scope: private | STRING |
|
|
|
| Description: name of the old-style mask grid function
|
|
|
|
| Range | | Default: SpaceMask::emask |
| .+ | any valid Cactus grid function name
|
|
|
|
| |
|
|
|
| old_style_mask_inside_value | Scope: private | REAL |
|
|
|
| Description: set the old-style mask to this value in the ’inside’ region
|
|
|
|
| Range | | Default: 0.0 |
| *:* | any real number
|
|
|
|
| |
|
|
|
| old_style_mask_outside_value | Scope: private | REAL |
|
|
|
| Description: set the old-style mask to this value in the ’outside’ region
|
|
|
|
| Range | | Default: 1.0 |
| *:* | any real number
|
|
|
|
| |
|
|
|
| opendx_control_file_name_extension | Scope: private | STRING |
|
|
|
| Description: file name extension for OpenDX control files
|
|
|
|
| Range | | Default: dx |
| .+ | any nonempty string
|
|
|
|
| |
|
|
|
| origin_x | Scope: private | REAL |
|
|
|
| Description: global x coordinate of patch system origin
|
|
|
|
| Range | | Default: 0.0 |
| *:* | any real number
|
|
|
|
| |
|
|
|
| origin_y | Scope: private | REAL |
|
|
|
| Description: global y coordinate of patch system origin
|
|
|
|
| Range | | Default: 0.0 |
| *:* | any real number
|
|
|
|
| |
|
|
|
| origin_z | Scope: private | REAL |
|
|
|
| Description: global z coordinate of patch system origin
|
|
|
|
| Range | | Default: 0.0 |
| *:* | any real number
|
|
|
|
| |
|
|
|
| output_ascii_files | Scope: private | BOOLEAN |
|
|
|
| Description: output h and Theta(h) as ASCII files
|
|
|
|
| | | Default: yes |
|
|
|
| |
|
|
|
| output_bh_diagnostics | Scope: private | BOOLEAN |
|
|
|
| Description: should we output BH diagnostics to a data file for each AH found?
|
|
|
|
| | | Default: true |
|
|
|
| |
|
|
|
| output_ghost_zones_for_h | Scope: private | BOOLEAN |
|
|
|
| Description: should we include the patch system (angular) interpatch ghost zones in h data files?
|
|
|
|
| | | Default: false |
|
|
|
| |
|
|
|
| output_h_every | Scope: private | INT |
|
|
|
| Description: how often (in Cactus time steps) should we output h (0 to disable)?
|
|
|
|
| Range | | Default: 1 |
| | don’t output h at all
|
| 1:* | any integer >= 1
|
|
|
|
| |
|
|
|
| output_hdf5_files | Scope: private | BOOLEAN |
|
|
|
| Description: output h and Theta(h) as HDF5 files
|
|
|
|
| | | Default: no |
|
|
|
| |
|
|
|
| output_initial_guess | Scope: private | BOOLEAN |
|
|
|
| Description: should we output the initial guess back to the h data file?
|
|
|
|
| | | Default: false |
|
|
|
| |
|
|
|
| output_mean_curvature_every | Scope: private | INT |
|
|
|
| Description: how often (in Cactus time steps) should we output the mean_curvature(h) functions?
|
|
|
|
| Range | | Default: (none) |
| | don’t output mean_curvature(h) at all
|
| 1:* | any integer >= 1
|
|
|
|
| |
|
|
|
| output_opendx_control_files | Scope: private | BOOLEAN |
|
|
|
| Description: should we output OpenDX control files to allow reading of AHFinderDirect ’ASCII
(gnuplot)’ format data files?
|
|
|
|
| | | Default: true |
|
|
|
| |
|
|
|
| output_theta_every | Scope: private | INT |
|
|
|
| Description: how often (in Cactus time steps) should we output the Theta(h) functions?
|
|
|
|
| Range | | Default: (none) |
| | don’t output Theta(h) at all
|
| 1:* | any integer >= 1
|
|
|
|
| |
|
|
|
| patch_overlap_width | Scope: private | INT |
|
|
|
| Description: number of grid points that nominally-just-touching patches should overlap
|
|
|
|
| Range | | Default: 1 |
| 1:*:2
| any integer >= 0; current implementation requires that
it be odd
|
|
|
|
| |
|
|
|
| patch_system_type | Scope: private | KEYWORD |
|
|
|
| Description: what type of patch system should we use?
|
|
|
|
| Range | | Default: match Cactus grid symmetry |
| see [1] below
| choose automagically based on grid symmetries and the
patch system’s origin
|
| full sphere | full sphere, no symmetries
|
| +z hemisphere | mirror symmetry across z=0 plane
|
| see [1] below | 90 degree periodic rotation symmetry about z axis
|
| see [1] below | mirror symmetry across x=0 and y=0 planes
|
| see [1] below | mirror symmetry across x=0 and z=0 planes
|
| see [1] below
| 180 degree periodic rotation symmetry about z axis and
mirror symmetry across z=0 plane
|
| see [1] below
| 90 degree periodic rotation symmetry about z axis and
mirror symmetry across z=0 plane
|
| see [1] below | mirror symmetry across x=0 and y=0 and z=0 planes
|
|
|
|
| |
[1]
match Cactus grid symmetry
[1]
+xy quadrant (rotating)
[1]
+xy quadrant (mirrored)
[1]
+xz quadrant (mirrored)
[1]
+xz quadrant (rotating)
[1]
+xyz octant (rotating)
[1]
+xyz octant (mirrored)
|
|
|
| predict_origin_movement | Scope: private | BOOLEAN |
|
|
|
| Description: predict origin movement when moving the origins
|
|
|
|
| | | Default: no |
|
|
|
| |
|
|
|
| pretracking_delta | Scope: private | REAL |
|
|
|
| Description: step size for value
|
|
|
|
| Range | | Default: 1.0 |
| (0.0:* |
|
|
|
|
| |
|
|
|
| pretracking_max_iterations | Scope: private | INT |
|
|
|
| Description: maximum number of pretracking iterations
|
|
|
|
| Range | | Default: 100 |
| 0:* |
|
|
|
|
| |
|
|
|
| pretracking_maximum_delta | Scope: private | REAL |
|
|
|
| Description: maximum step size for value
|
|
|
|
| Range | | Default: 1.0 |
| (0.0:* |
|
|
|
|
| |
|
|
|
| pretracking_maximum_value | Scope: private | REAL |
|
|
|
| Description: maximum pretracking value (should be near the outer boundary)
|
|
|
|
| Range | | Default: 10.0 |
| *:* |
|
|
|
|
| |
|
|
|
| pretracking_minimum_delta | Scope: private | REAL |
|
|
|
| Description: minimum step size for value
|
|
|
|
| Range | | Default: 1.0e-4 |
| (0.0:* |
|
|
|
|
| |
|
|
|
| pretracking_minimum_value | Scope: private | REAL |
|
|
|
| Description: minimum pretracking value
|
|
|
|
| Range | | Default: 0.0 |
| *:* |
|
|
|
|
| |
|
|
|
| pretracking_value | Scope: private | REAL |
|
|
|
| Description: initial pretracking value
|
|
|
|
| Range | | Default: 1.0 |
| *:* |
|
|
|
|
| |
|
|
|
| print_timing_stats | Scope: private | BOOLEAN |
|
|
|
| Description: should we print timing stats for the whole apparent-horizon-finding process?
|
|
|
|
| | | Default: false |
|
|
|
| |
|
|
|
| reset_horizon_after_not_finding | Scope: private | BOOLEAN |
|
|
|
| Description: reset the horizon shape to the initial data if a horizon was not found
|
|
|
|
| | | Default: yes |
|
|
|
| |
|
|
|
| reshape_while_moving | Scope: private | BOOLEAN |
|
|
|
| Description: reshape the horizons when moving them
|
|
|
|
| | | Default: no |
|
|
|
| |
|
|
|
| run_at_cctk_analysis | Scope: private | BOOLEAN |
|
|
|
| Description: should we run at CCTK_ANALYSIS?
|
|
|
|
| | | Default: false |
|
|
|
| |
|
|
|
| run_at_cctk_post_recover_variables | Scope: private | BOOLEAN |
|
|
|
| Description: should we run at CCTK_POST_RECOVER_VARIABLES?
|
|
|
|
| | | Default: false |
|
|
|
| |
|
|
|
| run_at_cctk_postinitial | Scope: private | BOOLEAN |
|
|
|
| Description: should we run at CCTK_POSTINITIAL?
|
|
|
|
| | | Default: false |
|
|
|
| |
|
|
|
| run_at_cctk_postpostinitial | Scope: private | BOOLEAN |
|
|
|
| Description: should we run at CCTK_POSTPOSTINITIAL?
|
|
|
|
| | | Default: false |
|
|
|
| |
|
|
|
| run_at_cctk_poststep | Scope: private | BOOLEAN |
|
|
|
| Description: should we run at CCTK_POSTSTEP?
|
|
|
|
| | | Default: true |
|
|
|
| |
|
|
|
| set_mask_for_all_horizons | Scope: private | BOOLEAN |
|
|
|
| Description: should we set a mask grid function (or functions) for all horizons?
|
|
|
|
| | | Default: false |
|
|
|
| |
|
|
|
| set_mask_for_individual_horizon | Scope: private | BOOLEAN |
|
|
|
| Description: should we set a mask grid function (or functions) for *this* horizon?
|
|
|
|
| | | Default: false |
|
|
|
| |
|
|
|
| set_new_style_mask | Scope: private | BOOLEAN |
|
|
|
| Description: if we’re setting a mask, should we set an new-style (CCTK_INT) mask gridfn?
|
|
|
|
| | | Default: false |
|
|
|
| |
|
|
|
| set_old_style_mask | Scope: private | BOOLEAN |
|
|
|
| Description: if we’re setting a mask, should we set an old-style (CCTK_REAL) mask gridfn?
|
|
|
|
| | | Default: true |
|
|
|
| |
|
|
|
| shiftout_factor | Scope: private | REAL |
|
|
|
| Description: enlarge the surface initial guess before finding
|
|
|
|
| Range | | Default: 1.0 |
| (0:*
| choose 1 for doing nothing, larger for enlarging, smaller
for shrinking
|
|
|
|
| |
|
|
|
| smoothing_factor | Scope: private | REAL |
|
|
|
| Description: smoothen (remove higher multipole moments) the surface initial guess before finding
|
|
|
|
| Range | | Default: 0.0 |
| *:*
| choose 0 for no smoothing, 1 for complete smoothing,
larger for over-smoothing, negative for roughening
|
|
|
|
| |
|
|
|
| surface_definition | Scope: private | KEYWORD |
|
|
|
| Description: search for what kind of surface?
|
|
|
|
| Range | | Default: expansion |
| expansion | Theta_(l) (apparent horizons etc.)
|
| inner expansion | Theta_(n) (expansion of ingoing null normal)
|
| mean curvature | for CMC surfaces
|
| expansion product | Theta_(l) Theta_(n) (product of the expansions)
|
|
|
|
| |
|
|
|
| surface_interpolator_name | Scope: private | STRING |
|
|
|
| Description: name under which the surface interpolation operator is registered in Cactus
|
|
|
|
| Range | | Default: Lagrange polynomial interpolation |
| | the empty string if this interpolator isn’t going to be used
|
| .+ | any string (in practice it should be nonempty)
|
|
|
|
| |
|
|
|
| surface_interpolator_pars | Scope: private | STRING |
|
|
|
| Description: parameters for the surface interpolator
|
|
|
|
| Range | | Default: order=2 boundary_off_centering_tolerance={1.0e-10 1.0e-10 1.0e-10 1.0e-10} boundary_extrapolation_tolerance={0.0 0.0 0.0 0.0} |
| .*
| ”any string acceptable to Util_TableSetFromStr ing()
and to the interpolator”
|
|
|
|
| |
|
|
|
| surface_modification | Scope: private | KEYWORD |
|
|
|
| Description: how to modify the surface definition
|
|
|
|
| Range | | Default: none |
| none | no modification |
| radius
| multiply with the coordinate radius
|
radius  | multiply with the square of the coordinate radius
|
| mean radius | multiply with the mean coordinate radius
|
| areal radius
| multiply with the areal radius (does not converge nicely,
because the Jacobian is only approximate)
|
|
|
|
| |
|
|
|
| surface_selection | Scope: private | KEYWORD |
|
|
|
| Description: search for a surface with this areal radius
|
|
|
|
| Range | | Default: definition |
| definition | ”look for a surface as defined by ’surface_definition’ ”
|
| see [1] below
| look for a surface with a certain mean coordinate radius
(not covariant, but fast)
|
| areal radius | look for a surface with a certain areal radius
|
| see [1] below
| look for a surface with a certain product of expansion
and mean coordiante radius
|
| see [1] below
| look for a surface with a certain product of expansion
and areal radius
|
|
|
|
| |
[1]
mean coordinate radius
[1]
expansion times mean coordinate radius
[1]
expansion times areal radius
|
|
|
| test_all_jacobian_compute_methods | Scope: private | BOOLEAN |
|
|
|
| Description: should we test all Jacobian computation methods, or just NP?
|
|
|
|
| | | Default: true |
|
|
|
| |
|
|
|
| theta_base_file_name | Scope: private | STRING |
|
|
|
| Description: base file name for Theta(h) output file(s)
|
|
|
|
| Range | | Default: Theta |
| .+ | any nonempty string
|
|
|
|
| |
|
|
|
| theta_norm_for_convergence | Scope: private | REAL |
|
|
|
| Description: we declare the horizon to be found if ——Theta——_infinity <= this
|
|
|
|
| Range | | Default: 1.0e-8 |
| (0.0:* | any positive real number
|
|
|
|
| |
|
|
|
| track_origin_from_grid_scalar | Scope: private | BOOLEAN |
|
|
|
| Description: track horizon origin from given grid scalars
|
|
|
|
| | | Default: no |
|
|
|
| |
|
|
|
| track_origin_source_x | Scope: private | STRING |
|
|
|
| Description: grid scalar containing the x component of the origin estimate
|
|
|
|
| Range | | Default: (none) |
| | don’t use this feature
|
| see [1] below | name of a grid scalar
|
|
|
|
| |
[1]
[a-zA-Z\_][a-zA-Z0-9\_]*[:][:][a-zA-Z\_][a-zA-Z0-9\_]*({\textbackslash}[0-9
+{\textbackslash}])
|
|
|
| track_origin_source_y | Scope: private | STRING |
|
|
|
| Description: grid scalar containing the x component of the origin estimate
|
|
|
|
| Range | | Default: (none) |
| | don’t use this feature
|
| see [1] below | name of a grid scalar
|
|
|
|
| |
[1]
[a-zA-Z\_][a-zA-Z0-9\_]*[:][:][a-zA-Z\_][a-zA-Z0-9\_]*({\textbackslash}[0-9
+{\textbackslash}])
|
|
|
| track_origin_source_z | Scope: private | STRING |
|
|
|
| Description: grid scalar containing the x component of the origin estimate
|
|
|
|
| Range | | Default: (none) |
| | don’t use this feature
|
| see [1] below | name of a grid scalar
|
|
|
|
| |
[1]
[a-zA-Z\_][a-zA-Z0-9\_]*[:][:][a-zA-Z\_][a-zA-Z0-9\_]*({\textbackslash}[0-9
+{\textbackslash}])
|
|
|
| umfpack__n_ii_iterations | Scope: private | INT |
|
|
|
| Description: number of iterative-improvement iterations to do inside UMFPACK after the sparse
LU decompose/solve, each time we solve a linear system
|
|
|
|
| Range | | Default: (none) |
| -1 | use the UMFPACK default
|
| | don’t do iterative improvement
|
| 1:*
| any positive integer (in practice a few iterations give
almost all the benefit)
|
|
|
|
| |
|
|
|
| use_pretracking | Scope: private | BOOLEAN |
|
|
|
| Description: search for an outermost apparent horizon
|
|
|
|
| | | Default: no |
|
|
|
| |
|
|
|
| verbose_level | Scope: private | KEYWORD |
|
|
|
| Description: controls which (how many) messages to print describing AH finding
|
|
|
|
| Range | | Default: physics details |
| physics highlights | just a few physics messages
|
| physics details | more detailed physics messages
|
| algorithm highlights
| physics details + a few messages about the AH-finding
algorithm
|
| algorithm details
| physics details + lots of messages about the AH-finding
algorithm
|
| algorithm debug
| physics details + lots and lots of messages about the
AH-finding algorithm
|
|
|
|
| |
|
|
|
| want_expansion_gradients | Scope: private | BOOLEAN |
|
|
|
| Description: should we print the gradients of the expansions?
|
|
|
|
| | | Default: false |
|
|
|
| |
|
|
|
| warn_level__gij_not_positive_definite__initial | Scope: private | INT |
|
|
|
| Description: warning level if the interpolated g_{ij} isn’t positive definite (usually this means
we’re too close to a singularity) (error occurs on first Newton iteration)
|
|
|
|
| Range | | Default: 2 |
| -1:* | any valid Cactus warning level
|
|
|
|
| |
|
|
|
| warn_level__gij_not_positive_definite__subsequent | Scope: private | INT |
|
|
|
| Description: warning level if the interpolated g_{ij} isn’t positive definite (usually this means
we’re too close to a singularity) (error occurs on subsequent Newton iteration)
|
|
|
|
| Range | | Default: 2 |
| -1:* | any valid Cactus warning level
|
|
|
|
| |
|
|
|
| warn_level__nonfinite_geometry | Scope: private | INT |
|
|
|
| Description: warning level if we find infinity and/or NaN in the interpolated geometry values
{g_ij, partial_k g_ij, K_ij}
|
|
|
|
| Range | | Default: 1 |
| -1:* | any valid Cactus warning level
|
|
|
|
| |
|
|
|
| warn_level__point_outside__initial | Scope: private | INT |
|
|
|
| Description: warning level for point outside (or too close to boundary of) Cactus grid (error
occurs on first Newton iteration)
|
|
|
|
| Range | | Default: 1 |
| -1:* | any valid Cactus warning level
|
|
|
|
| |
|
|
|
| warn_level__point_outside__subsequent | Scope: private | INT |
|
|
|
| Description: warning level for point outside (or too close to boundary of) Cactus grid (error
occurs on subsequent Newton iteration)
|
|
|
|
| Range | | Default: 2 |
| -1:* | any valid Cactus warning level
|
|
|
|
| |
|
|
|
| warn_level__skipping_finite_check | Scope: private | INT |
|
|
|
| Description: warning level if the user sets check_that_geometry_is_finite but the Cactus configure
process doesn’t find a finite() function so we have to skip the finite-geometry check
|
|
|
|
| Range | | Default: 3 |
| -1:* | any valid Cactus warning level
|
|
|
|
| |
|
|
|
| which_horizon_to_announce_centroid | Scope: private | INT |
|
|
|
| Description: for which horizon should we announce the centroid?
|
|
|
|
| Range | | Default: (none) |
| | don’t announce any centroid(s)
|
| 1:100 | announce this horizon’s centroid each time we find it
|
|
|
|
| |
|
|
|
| which_surface_to_store_info | Scope: private | INT |
|
|
|
| Description: into which surface should we store the info?
|
|
|
|
| Range | | Default: -1 |
| -1 | don’t store info
|
| 0:* | store info into the corresponding surface
|
|
|
|
| |
|
|
|
| which_surface_to_store_info_by_name | Scope: private | STRING |
|
|
|
| Description: into which surface should we store the info?
|
|
|
|
| Range | | Default: (none) |
| | ”use which_surface_to_sto re_info”
|
| .* | any string
|
|
|
|
| |
|
|
|
| maxnphi | Scope: shared from SPHERICALSURFACE | INT |
|
|
|
| |
|
|
|
| maxntheta | Scope: shared from SPHERICALSURFACE | INT |
|
|
|
| |
|
|
|
| nsurfaces | Scope: shared from SPHERICALSURFACE | INT |
|
|
|
| |
15 Interfaces
General
Implements:
ahfinderdirect
Inherits:
grid
admbase
staticconformal
spacemask
sphericalsurface
io
Grid Variables
15.0.1 PRIVATE GROUPS
|
|
|
|
| Group Names | Variable Names | Details | |
|
|
|
|
| ahmask | ahmask | compact | 0 |
| | | dimensions | 3 |
| | | distribution | DEFAULT |
| | | group type | GF |
| | | tags | tensortypealias=”Scalar” Prolongation=”None” InterpNumTimelevels=1 |
| | | timelevels | 3 |
|
| | variable type | REAL |
|
|
|
|
|
ah_radius | ah_radius | compact | 0 |
| | | dimensions | 3 |
| | | distribution | CONSTANT |
|
| | group type | ARRAY |
|
| | size | MAX_N_ZONES_PER_RIGHT_ANGLE+1 |
|
| | size | MAX_N_ZONES_PER_RIGHT_ANGLE+1 |
| | | size | 6 |
| | | timelevels | 1 |
|
| | vararray_size | N_horizons |
|
| | variable type | REAL |
|
|
|
|
|
ah_origin | | compact | 0 |
|
| ah_origin_x | dimensions | 0 |
| | ah_origin_y | distribution | CONSTANT |
| | ah_origin_z | group type | SCALAR |
| | | timelevels | 1 |
| | | vararray_size | N_horizons |
| | | variable type | REAL |
|
|
|
|
| ah_centroid | | compact | 0 |
| | ah_centroid_x | dimensions | 0 |
| | ah_centroid_y | distribution | CONSTANT |
| | ah_centroid_z | group type | SCALAR |
| | ah_centroid_t | timelevels | 1 |
| | ah_centroid_x_p | vararray_size | N_horizons |
| | ah_centroid_y_p | variable type | REAL |
|
|
|
|
| ah_flags | | compact | 0 |
| | ah_initial_find_flag | dimensions | 0 |
| | ah_really_initial_find_flag | distribution | CONSTANT |
| | ah_search_flag | group type | SCALAR |
| | ah_found_flag | timelevels | 1 |
| | ah_centroid_valid | vararray_size | N_horizons |
| | ah_centroid_valid_p | variable type | INT |
|
|
|
|
| |
Uses header:
SpaceMask.h
Provides:
HorizonLocalCoordinateOrigin to
HorizonWasFound to
HorizonCentroid to
HorizonRadiusInDirection to
16 Schedule
This section lists all the variables which are assigned storage by thorn EinsteinAnalysis/AHFinderDirect.
Storage can either last for the duration of the run (Always means that if this thorn is activated storage will
be assigned, Conditional means that if this thorn is activated storage will be assigned for the
duration of the run if some condition is met), or can be turned on for the duration of a schedule
function.
Storage
| Always: | |
| ah_radius ah_origin ah_centroid ah_flags | |
| ahmask[1] | |
| | |
| |
Scheduled Functions
CCTK_BASEGRID
ahfinderdirect_setup
setup data structures
| | After: | spatialcoordinates |
| | Language: | c |
| | Options: | global |
| | Type: | function |
| | Writes: | ahfinderdirect::ah_centroid |
| | | ah_flags |
| |
CCTK_POST_RECOVER_VARIABLES (conditional)
ahfinderdirect_recover
import horizon data from cactus variables
| | Language: | c |
| | Options: | global |
| | Type: | function |
| |
CCTK_ANALYSIS (conditional)
ahfinderdirect_announce
announce horizon position(s) to other thorns
| | After: | ahfinderdirect_find_horizons |
| | Before: | driftcorrect |
| | Language: | c |
| | Options: | global-early |
| | Type: | function |
| |
CCTK_ANALYSIS (conditional)
ahfinderdirect_maybe_do_masks
set mask(s) based on apparent horizon position(s)
| | After: | ahfinderdirect_find_horizons |
| | Language: | c |
| | Type: | function |
| |
CCTK_POSTSTEP (conditional)
ahfinderdirect_import_mask
import the excision mask
| | Before: | ahfinderdirect_find_horizons |
| | Language: | c |
| | Options: | global-early |
| | | loop-local |
| | Reads: | spacemask::emask |
| | Type: | function |
| | Writes: | ahfinderdirect::ahmask(everywhere) |
| |
CCTK_POSTSTEP (conditional)
ahfinderdirect_store
store apparent horizon(s) into spherical surface(s)
| | After: | ahfinderdirect_find_horizons |
| | Before: | sphericalsurface_hasbeenset |
| | Language: | c |
| | Options: | global-early |
| | Type: | function |
| |
CCTK_POSTSTEP (conditional)
ahfinderdirect_save
save apparent horizon(s) into cactus variables
| | After: | ahfinderdirect_find_horizons |
| | Language: | c |
| | Options: | global-early |
| | Type: | function |
| |
CCTK_POSTSTEP (conditional)
ahfinderdirect_announce
announce horizon position(s) to other thorns
| | After: | ahfinderdirect_find_horizons |
| | Before: | driftcorrect |
| | Language: | c |
| | Options: | global-early |
| | Type: | function |
| |
CCTK_POSTSTEP (conditional)
ahfinderdirect_maybe_do_masks
set mask(s) based on apparent horizon position(s)
| | After: | ahfinderdirect_find_horizons |
| | Language: | c |
| | Type: | function |
| |
CCTK_POSTINITIAL (conditional)
ahfinderdirect_import_mask
import the excision mask
| | Before: | ahfinderdirect_find_horizons |
| | Language: | c |
| | Options: | global-early |
| | | loop-local |
| | Reads: | spacemask::emask |
| | Type: | function |
| | Writes: | ahfinderdirect::ahmask(everywhere) |
| |
CCTK_POSTINITIAL (conditional)
ahfinderdirect_store
store apparent horizon(s) into spherical surface(s)
| | After: | ahfinderdirect_find_horizons |
| | Before: | sphericalsurface_hasbeenset |
| | Language: | c |
| | Options: | global-early |
| | Type: | function |
| |
CCTK_POSTINITIAL (conditional)
ahfinderdirect_save
save apparent horizon(s) into cactus variables
| | After: | ahfinderdirect_find_horizons |
| | Language: | c |
| | Options: | global-early |
| | Type: | function |
| |
CCTK_ANALYSIS (conditional)
ahfinderdirect_find_horizons
find apparent horizon(s) after this time step
| | Language: | c |
| | Options: | global-early |
| | Reads: | staticconformal::conformal_state |
| | Type: | function |
| |
CCTK_POSTINITIAL (conditional)
ahfinderdirect_announce
announce horizon position(s) to other thorns
| | After: | ahfinderdirect_find_horizons |
| | Before: | driftcorrect |
| | Language: | c |
| | Options: | global-early |
| | Type: | function |
| |
CCTK_POSTINITIAL (conditional)
ahfinderdirect_maybe_do_masks
set mask(s) based on apparent horizon position(s)
| | After: | ahfinderdirect_find_horizons |
| | Language: | c |
| | Type: | function |
| |
CCTK_POSTPOSTINITIAL (conditional)
ahfinderdirect_import_mask
import the excision mask
| | Before: | ahfinderdirect_find_horizons |
| | Language: | c |
| | Options: | global-early |
| | | loop-local |
| | Reads: | spacemask::emask |
| | Type: | function |
| | Writes: | ahfinderdirect::ahmask(everywhere) |
| |
CCTK_POSTPOSTINITIAL (conditional)
ahfinderdirect_store
store apparent horizon(s) into spherical surface(s)
| | After: | ahfinderdirect_find_horizons |
| | Language: | c |
| | Options: | global-early |
| | Type: | function |
| |
CCTK_POSTPOSTINITIAL (conditional)
ahfinderdirect_save
save apparent horizon(s) into cactus variables
| | After: | ahfinderdirect_find_horizons |
| | Language: | c |
| | Options: | global-early |
| | Type: | function |
| |
CCTK_POSTPOSTINITIAL (conditional)
ahfinderdirect_announce
announce horizon position(s) to other thorns
| | After: | ahfinderdirect_find_horizons |
| | Before: | driftcorrect |
| | Language: | c |
| | Options: | global-early |
| | Type: | function |
| |
CCTK_POSTPOSTINITIAL (conditional)
ahfinderdirect_maybe_do_masks
set mask(s) based on apparent horizon position(s)
| | After: | ahfinderdirect_find_horizons |
| | Language: | c |
| | Type: | function |
| |
CCTK_POST_RECOVER_VARIABLES (conditional)
ahfinderdirect_import_mask
import the excision mask
| | Before: | ahfinderdirect_find_horizons |
| | Language: | c |
| | Options: | global-early |
| | | loop-local |
| | Reads: | spacemask::emask |
| | Type: | function |
| | Writes: | ahfinderdirect::ahmask(everywhere) |
| |
CCTK_POST_RECOVER_VARIABLES (conditional)
ahfinderdirect_store
store apparent horizon(s) into spherical surface(s)
| | After: | ahfinderdirect_find_horizons |
| | Before: | sphericalsurface_hasbeenset |
| | Language: | c |
| | Options: | global-early |
| | Type: | function |
| |
CCTK_POST_RECOVER_VARIABLES (conditional)
ahfinderdirect_save
save apparent horizon(s) into cactus variables
| | After: | ahfinderdirect_find_horizons |
| | Language: | c |
| | Options: | global-early |
| | Type: | function |
| |
CCTK_POSTSTEP (conditional)
ahfinderdirect_find_horizons
find apparent horizon(s) after this time step
| | Language: | c |
| | Options: | global-early |
| | Type: | function |
| |
CCTK_POST_RECOVER_VARIABLES (conditional)
ahfinderdirect_announce
announce horizon position(s) to other thorns
| | After: | ahfinderdirect_find_horizons |
| | Before: | driftcorrect |
| | Language: | c |
| | Options: | global-early |
| | Type: | function |
| |
CCTK_POST_RECOVER_VARIABLES (conditional)
ahfinderdirect_maybe_do_masks
set mask(s) based on apparent horizon position(s)
| | After: | ahfinderdirect_find_horizons |
| | Language: | c |
| | Type: | function |
| |
CCTK_POSTREGRIDINITIAL
ahfinderdirect_maybe_do_masks
set mask(s) based on apparent horizon position(s)
| | After: | maskone |
| | | maskzero |
| | Language: | c |
| | Type: | function |
| |
CCTK_POSTREGRID
ahfinderdirect_maybe_do_masks
set mask(s) based on apparent horizon position(s)
| | After: | maskone |
| | | maskzero |
| | Language: | c |
| | Type: | function |
| |
CCTK_POSTINITIAL (conditional)
ahfinderdirect_find_horizons
find apparent horizon(s) after this time step
| | Language: | c |
| | Options: | global-early |
| | Type: | function |
| |
CCTK_POSTPOSTINITIAL (conditional)
ahfinderdirect_find_horizons
find apparent horizon(s) after this time step
| | Language: | c |
| | Options: | global-early |
| | Type: | function |
| |
CCTK_POST_RECOVER_VARIABLES (conditional)
ahfinderdirect_find_horizons
find apparent horizon(s) after this time step
| | After: | mol_poststep |
| | Language: | c |
| | Options: | global-early |
| | Type: | function |
| |
CCTK_ANALYSIS (conditional)
ahfinderdirect_import_mask
import the excision mask
| | Before: | ahfinderdirect_find_horizons |
| | Language: | c |
| | Options: | global-early |
| | | loop-local |
| | Reads: | spacemask::emask |
| | Type: | function |
| | Writes: | ahfinderdirect::ahmask(everywhere) |
| |
CCTK_ANALYSIS (conditional)
ahfinderdirect_store
store apparent horizon(s) into spherical surface(s)
| | After: | ahfinderdirect_find_horizons |
| | Before: | sphericalsurface_hasbeenset |
| | Language: | c |
| | Options: | global-early |
| | Type: | function |
| |
CCTK_ANALYSIS (conditional)
ahfinderdirect_save
save apparent horizon(s) into cactus variables
| | After: | ahfinderdirect_find_horizons |
| | Language: | c |
| | Options: | global-early |
| | Type: | function |
| |
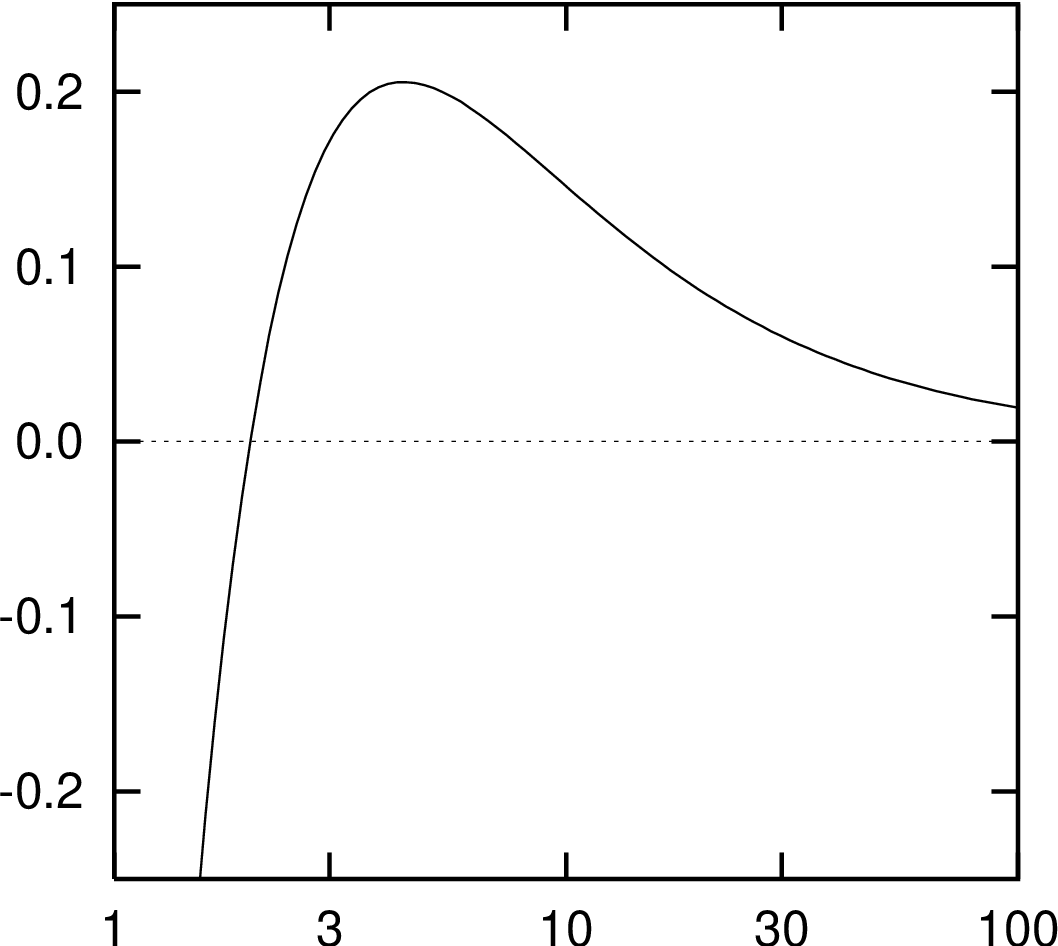
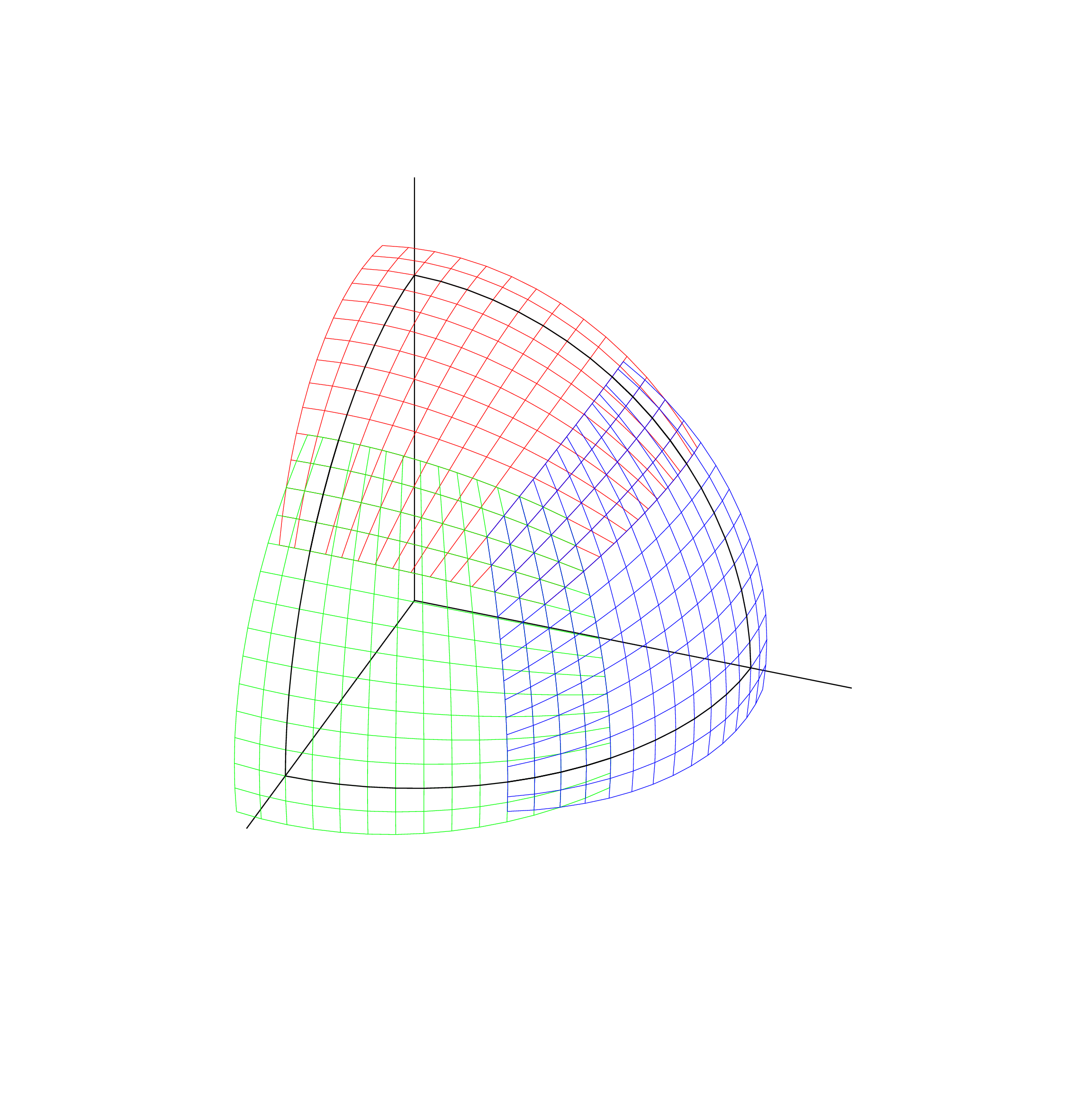







 = any real number with
absolute value
= any real number with
absolute value 
 = any real number with
absolute value
= any real number with
absolute value 
