Finding Apparent Horizons in a numerical spacetime
Thorn AHFinder finds Apparent Horizons (AHs) in numerical spacetimes. It calulates various quantities like horizon area and its corresponding mass.
Thorn AHFinder can be used either with a minimization or a flow algorithm.
ahfinder::ahf_active (steerable)
To activate the thorn set ahf_active = ”yes”. This parameter is set by default to ”no”.
ahfinder::ahf_flow (steerable)
By default the minimization algorithm is used. To switch to the flow algorithm one has to set
ahf_flow = ”yes”
ahfinder::ahf_findevery (steerable)
Specifies how often the finder is called. The default is to find horizons at every iteration.
ahfinder::ahf_findafter (steerable)
The number of iterations after which the thorn is called the first time can be specified by this
parameter. Here the default is 0, calling the thorn also on the initial time slice.
ahfinder::ahf_findaftertime
Instead of specifying the number of iterations, one can specify after how much coordinate time
the thorn is called the first time. When different from zero, this parameter overrides the value of
ahf_findafter. Default here is also 0.
ahfinder::ahf_lmax
The maximal number of terms in the expansion in \(\theta \). The default value is 8. The maximal value is
19.
ahfinder::ahf_phi (steerable)
If axisymmetry is expected the surface does not need to be expanded in phi. This is the default. To
look for non-axisymmetric surface use ahf_phi = ”yes”.
ahfinder::ahf_[xyz]c (steerable)
Sets the x-, y-, and z-coordinates of the center of the expansion. The default is the origin (ahf_xc =
0, ahf_yc = 0, ahf_zc = 0). The center of the expansion should be set inside the expected apparent
horizon, otherwise the algorithm will fail.
ahfinder::ahf_wander
The center of the expansion can also be allowed to move. To do this use ahf_wander = ”yes”.
However, this only works with the minimization algorithm. The default is for the center not to
move.
ahfinder::ahf_r0 (steerable)
Sets the radius of the initial sphere. The default is 0.0, forcing the largest sphere possible in the
grid.
The finder can also be used to look for three horizons each time. This is done by just running the algorithm three consecutive times with different initial guesses, and is useful for simulations of black hole collisions.
ahfinder::ahf_find3
Set ahf_find3 = ”yes” to search for three horizons. The default is to look for only one horizon.
ahfinder::ahf_[xyz]_[012] (steerable)
Sets the x-, y-, and z-coordinates of the center of the expansion for horizon 0, 1 and 2. The default
in each case is the origin.
ahfinder::ahf_r0_[0-2] (steerable)
Sets the radius of the initial spheres for horizon 0, 1 and 2. The default in all cases is 0.0, forcing
the largest sphere possible in the grid.
The initial guess can be furthermore controlled by some parameters which are set to ”no” by default.
ahfinder::ahf_guessold (steerable)
To use on old horizon as initial guess set ahf_guessold = ”yes”. However, if during the evolution
the apparent horizon jumps discontinuously it might be lost by using this option.
ahfinder::ahf_nn0, ahfinder::ahf_nn2
If no old horizon is used the inital guess can be specified further for the minimization algorithm.
This algorithm is sensitive to the initial guess, so this is important. The initial guess is set up by an
expansion in spherical harmonics in the first two coefficients (l=0,l=2). The default for both these
parameters are 10, in which case the algorithm tests 100 different combinations to find the best
initial guess.
ahfinder::ahf_sloppyguess
It is also possible to use only a sphere as initial guess. This is much faster and is done by using
ahf_sloppyguess = ”yes”. In this case a number of spheres (specified by ahf_nn0) with different
radii are tested for the initial guess.
ahfinder::ahf_inner
If one wants to look for an inner horizon instead of an outer one, use ahfinder::ahf_inner = ”yes”.
This only works with the minimization algorithm.
ahfinder::ahf_ntheta (steerable)
The number of subdivisions in \(\theta \). Default is 200.
ahfinder::ahf_nphi (steerable)
The number of subdivisions in \(\phi \). Default is 200.
ahfinder::ahf_ref[xyz] (steerable)
Specifies the existence of reflection symmetry on the yz-plane, xz-plane and xy-plane respectively.
By default all are set to ”no”.
ahfinder::ahf_octant (steerable)
Octant symmetry is specified by using ahf_octant = ”yes”. This is set to ”no” by default. Possible
parmeter settings are ”yes” for reflection symmetries on all three coordinate planes and ”high” for
an additional rotational symmetry of \(\pi /2\) around the z axis.
ahfinder::ahf_cartoon (steerable)
A further symmetry can (must) be specified when running with the ”axisymmetric” mode given by
the Cartoon method by using ahf_cartoon = ”yes”. This is set to ”no” by default.
ahfinder::ahf_tol
Sets the tolerance for the minimization algorithm. The default value is 0.1.
ahfinder::ahf_maxiter
Sets the maximum number if iterations for each step of the POWELL algorithm. The default value
is 10.
ahfinder::ahf_minarea
Usually the square of the expansion is minimized. To switch to minimization of the area one can
use ahf_minarea = ”yes” (default is ”no”). Notice that only for time symmetric data the surface
found by area minimization will correspond to an apparent horizon.
ahfinder::ahf_flow (steerable)
The fow algotithm is used by setting ahf_flow = ”yes”. The default is ”no”
ahfinder::ahf_flowiter (steerable)
Sets the maximum number of iterations for the flow algorithm. The default value is 200.
ahfinder::ahf_flowtol
Sets the tolerance for the flow. The default value is 0.0001.
ahfinder::ahf_flowa
Sets the \(\alpha \) parameter for the flow. The default value is 0.01.
ahfinder::ahf_flowb
Sets the \(\beta \) parameter for the flow. The default value is 0.5.
ahfinder::ahf_flowh
Sets the weight of \(H\) flow. The default value is 0.0.
ahfinder::ahf_flowc
Sets the weight of \(C\) flow. The default value is 1.0.
ahfinder::ahf_flown
Sets the weight of \(N\) flow (not yet implemented). The default value is 0.0.
The character of the different flows and the \(\alpha \) and \(\beta \) parameters are described in Carsten Gundlach’s paper on his pseudo-spectral apparent horizon finder (gr-qc/9707050).
ahfinder::ahf_logfile
By default no logfile for AHFinder is written. To obtain a log file one must set ahf_logfile = ”yes”.
ahfinder::ahf_verbose
if ahf_verbose = ”yes” messages are printed to screen at the beginning and the end of the algorithm.
This is the default.
ahfinder::ahf_veryverbose
if ahf_veryverbose = ”yes” messages are also printed to screen during the iteration process. The
default is ”no”.
ahfinder::ahf_2Doutput (steerable)
To get 2D output of grid functions use ahf_2Doutput = ”yes” (default is ”no”). The output is
controlled be the thorn itself, not by cactus standard output.
ahfinder::ahf_3Doutput (steerable)
In future versions to get 3D output of grid functions use ahf_3Doutput = ”yes” (default is ”no”).
ahfinder::ahf_areamap
To get an area map use ahf_areamap = ”yes” (default is ”no”). This is useful for looking at the
behaviour of the area for surfaces close to the horizon.
ahfinder::ahf_mask (steerable)
The mask is 0 inside the horizon and 1 outside, and is used in black-hole excision techniques. By
default the mask is off. It can be enabled by setting ahf_mask = ”strong”, which sets the mask only
if the finder is sure that a horizon was found, or by setting ahf_mask = ”weak”, which makes the
finder set the mask also if a horizon is probably there but either the resolution or lmax are to low
to really resolve it.
ahfinder::ahf_masktype (steerable)
The mask can be of two types. Either ahf_masktype = ”simple”, which masks a cube contained
inside the horizons, or ahf_masktype = ”lego”, which masks a lego-sphere.
ahfinder::ahf_maskshrink (steerable)
Sets a buffer zone between the region inside the horizon and the region where the mask is 0, by
limiting the mask to a region smaller than ahf_maskshrink times the horizon radius. The default
value is 0.8.
ahfinder::ahf_maskbuffer (steerable)
Sets a buffer zone between the region inside the horizon and the region where the mask is 0 with a
width of at least ahf_maskbuffer grid points. The default value is 5.
Usually only a few of the parameters described above are needed in the parameter file. The simplest parameter settings for using the flow algorithm for a full 3D horizon with a large sphere as initial guess is
interpolation_order = 2 # Second order interpolation ahf_active = "yes" ahf_flow = "yes" ahf_phi = "yes"
This looks for a non-axisymmetric horizon around the origin with lmax = 8 and using the flow algorithm. It starts with the largest sphere that fits in the 3D grid and outputs 2D grid functions. The other parameters can be used if needed.
In full 3D the flow algorithm is faster than the minimization algorithm. However, in cases when there are very few terms in the expansion in spherical harmonics the minimization can be faster. In axisymmetry this typically happens for lmax\(\leq 10\).
While the default settings usually work fine, they can be changed to meet special purposes:
If the horizon is expected to be far from spherical the parameter ahf_lmax can be set to a higher value. 12 should be high enough. However, only values up to 20 are supported.
If the latter parameter is set to a value higher than 8 then the parameter ahf_maxiter can be raised to, e.g., 14. This can be useful since more iterations can be necessary for higher coefficients of the expansion.
The output of the thorn consists of two gridfunctions and several one dimensional output files.
To depict the position of the horizon, the most important files are ahfgrid_2d_...ieee. These files contain a 2D gridfunction whose zero level locates the horizon.
The files ahf_exp_2d_...ieee show the expansion of outgoing photons on the level set of the gridfunction ahfgrid. The horizon coincides with zeros of the expansion.
The surface area of the horizon is given in ahf_area.tl
The mass of the horizon is given in ahf_mass.tl
The coefficients of the expansion in spherical harmonics are given in ahf_coeff.alm.
The files ahf_circ_eq.tl, ahf_meri_p1.tl and ahf_meri_p2.tl contain the equatorial circumference of the surface, the length of the meridian at \(\phi =0\), and the length of the meridian at \(\phi =\pi /2\) of the surface, respectively.
If an output of a logfile is set in the parameters, the log file for the last time the horizon was called is ahf_logfile.
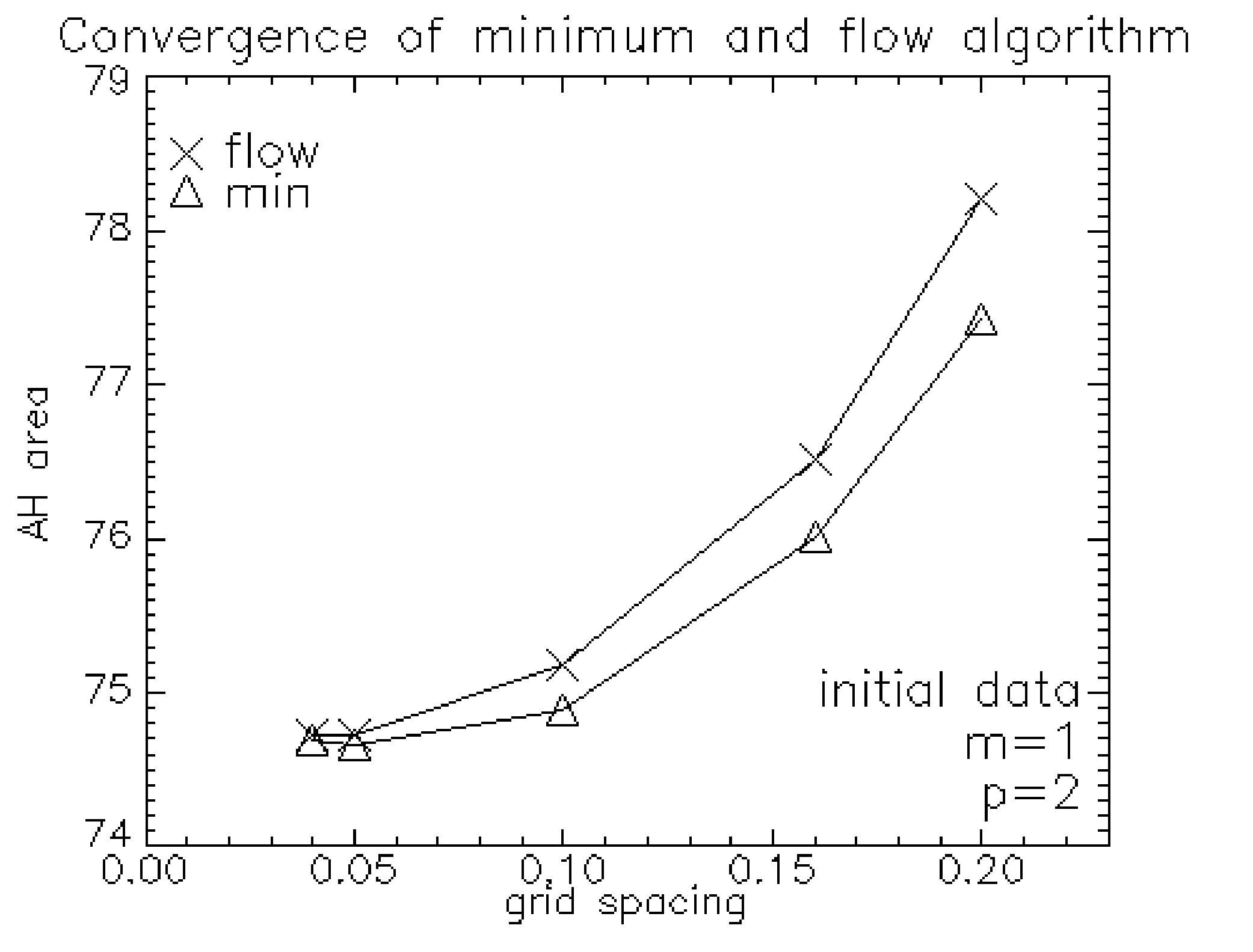
The finder has been examined with puncture initial data for single and binary-black hole scenarios.
Calculations with different grid spacings but constant grid size show convergence of the horizon area.
This has been checked with different linear momenta in the z direction \(P_{z}=(0M,2M,5M)\) and vanishing spin. Also for \(P_{z}=2M\) and a spin of \(5M\) in the x direction the horizon converges. Figure 1 shows the case with \(P_{z}=2M\) and vanishing spin.
Further, not only the area converges but also the shape of the horizon. For both the minimization and the flow algorithm the horizon converges to the same shape, as can be seen from the coefficients fo the expansion. The order of convergence for the coefficients is between 1.4 and 1.7.
By using the parameters ahf_xc, ahf_yc, ahf_zc it can also be shown that the finder also locates horizons which are not centered. This works in general as long as the surface can be expanded in spherical harmonics around this point, but the error increases with the off-centering.
The parameter ahf_r0 can be used e.g. when dealing with two black holes. If one searches for separate horizons one can center the finder on one of the locations of the holes and use an initial radius ahf_r0 smaller than the coordinate distance of the holes. With this parameter settings the single horizon can be found faster. But also a setup with an initial sphere of maximum radius should work at least for the flow algorithm. This has been checked with puncture data for two holes with vanishing linear and angular momentum for each hole (equivalent to Brill-Lindquist data) and is shown in Figure 2. Here for a coordinate distance of the holes of 1.6M the separated horizons for the holes are found but no common horizon. For a coordinate distance of 1.5M a common horizon is found and also single ones, which are inner surfaces in this case. This coincides with other work where the critical coordinate distance for a single horizon is between 1.53M and 1.56M (gr-qc/9809004).
The dashed lines show inner trapped surfaces in the left figure and the surface where the algorithm stopped without finding a horizon in the right figure.
Also the Misner case was checked. Here for \(\mu \) = 1.35 a common horizon is found. For \(\mu \) = 1.37 separated horizons are found. From the literature we know that (e.g. gr-qc/9809004) the critical value of \(\mu \) is 1.36. This is confirmed by the horizon finder.
The information of when a horizon was found can be seen in the cactus-logfile. There will be output from the thorn even if no horizon was found.
| ahf_1doutput | Scope: private | BOOLEAN |
| Description: 1D output of grid functions?
| ||
| Default: no | ||
| ahf_2doutput | Scope: private | BOOLEAN |
| Description: 2D output of grid functions?
| ||
| Default: no | ||
| ahf_3doutput | Scope: private | BOOLEAN |
| Description: 3D output of grid functions?
| ||
| Default: no | ||
| ahf_areamap | Scope: private | BOOLEAN |
| Description: Find area map?
| ||
| Default: no | ||
| ahf_cartoon | Scope: private | BOOLEAN |
| Description: Cartoon mode?
| ||
| Default: no | ||
| ahf_find3 | Scope: private | BOOLEAN |
| Description: Searching for 3 surfaces?
| ||
| Default: no | ||
| ahf_findafter | Scope: private | INT |
| Description: After how many iterations look for horizons
| ||
| Range | Default: (none) | |
| 0: | Any positive integer
| |
| ahf_findaftertime | Scope: private | REAL |
| Description: After how much time look for horizons
| ||
| Range | Default: 0.0 | |
| 0.0: | Any positive real number. If non-zero overides ahf_findafter
| |
| ahf_findevery | Scope: private | INT |
| Description: How often to look for horizons
| ||
| Range | Default: 1 | |
| 1: | Set to 1 for searching each iteration
| |
| ahf_flow | Scope: private | BOOLEAN |
| Description: Use flow instead of minimization?
| ||
| Default: no | ||
| ahf_flowa | Scope: private | REAL |
| Description: alpha parameter for flow
| ||
| Range | Default: 0.01 | |
| : | Anything
| |
| ahf_flowb | Scope: private | REAL |
| Description: beta parameter for flow
| ||
| Range | Default: 0.5 | |
| : | Anything
| |
| ahf_flowc | Scope: private | REAL |
| Description: Weight of C flow
| ||
| Range | Default: 1.0 | |
| : | Anything
| |
| ahf_flowh | Scope: private | REAL |
| Description: Weight of H flow
| ||
| Range | Default: 0.0 | |
| : | Anything
| |
| ahf_flowiter | Scope: private | INT |
| Description: Maximum number of iterations for flow
| ||
| Range | Default: 200 | |
| 0: | Anything
| |
| ahf_flown | Scope: private | REAL |
| Description: Weight of N flow
| ||
| Range | Default: 0.0 | |
| : | Anything
| |
| ahf_flowtol | Scope: private | REAL |
| Description: Tolerance for flow
| ||
| Range | Default: 0.0001 | |
| : | Anything
| |
| ahf_gaussout | Scope: private | BOOLEAN |
| Description: Output gaussian curvature of horizon?
| ||
| Default: yes | ||
| ahf_guess_absmin | Scope: private | BOOLEAN |
| Description: Use absolute min to start minimization?
| ||
| Default: no | ||
| ahf_guessold | Scope: private | BOOLEAN |
| Description: Use old horizon as initial guess?
| ||
| Default: no | ||
| ahf_guessverbose | Scope: private | BOOLEAN |
| Description: Print info on initial guess?
| ||
| Default: no | ||
| ahf_hdf5output | Scope: private | BOOLEAN |
| Description: HDF5 output of AHFinder data?
| ||
| Default: no | ||
| ahf_inner | Scope: private | BOOLEAN |
| Description: Look for inner horizon?
| ||
| Default: no | ||
| ahf_l0_guess | Scope: private | REAL |
| Description: Manual guess for l=0 component
| ||
| Range | Default: 1.0 | |
| : | Anything
| |
| ahf_l10_guess | Scope: private | REAL |
| Description: Manual guess for l=10 component
| ||
| Range | Default: 0.0 | |
| : | Anything
| |
| ahf_l12_guess | Scope: private | REAL |
| Description: Manual guess for l=12 component
| ||
| Range | Default: 0.0 | |
| : | Anything
| |
| ahf_l14_guess | Scope: private | REAL |
| Description: Manual guess for l=14 component
| ||
| Range | Default: 0.0 | |
| : | Anything
| |
| ahf_l16_guess | Scope: private | REAL |
| Description: Manual guess for l=16 component
| ||
| Range | Default: 0.0 | |
| : | Anything
| |
| ahf_l18_guess | Scope: private | REAL |
| Description: Manual guess for l=18 component
| ||
| Range | Default: 0.0 | |
| : | Anything
| |
| ahf_l2_guess | Scope: private | REAL |
| Description: Manual guess for l=2 component
| ||
| Range | Default: 0.0 | |
| : | Anything
| |
| ahf_l4_guess | Scope: private | REAL |
| Description: Manual guess for l=4 component
| ||
| Range | Default: 0.0 | |
| : | Anything
| |
| ahf_l6_guess | Scope: private | REAL |
| Description: Manual guess for l=6 component
| ||
| Range | Default: 0.0 | |
| : | Anything
| |
| ahf_l8_guess | Scope: private | REAL |
| Description: Manual guess for l=8 component
| ||
| Range | Default: 0.0 | |
| : | Anything
| |
| ahf_lmax | Scope: private | INT |
| Description: Maximum number of terms in theta expansion
| ||
| Range | Default: 8 | |
| 0:19 | Range from 0 to 19
| |
| ahf_logfile | Scope: private | BOOLEAN |
| Description: Write log file?
| ||
| Default: no | ||
| ahf_manual_guess | Scope: private | BOOLEAN |
| Description: Use specified coefficients for guess?
| ||
| Default: no | ||
| ahf_mask | Scope: private | KEYWORD |
| Description: Use mask?
| ||
| Range | Default: off | |
| off | Mask is off
| |
| strong | Mask set only for definite horizons
| |
| weak | Mask set for both definite and probable horizons
| |
| ahf_mask_0 | Scope: private | BOOLEAN |
| Description: Mask for first horizon with find3?
| ||
| Default: yes | ||
| ahf_mask_1 | Scope: private | BOOLEAN |
| Description: Mask for second horizon with find3?
| ||
| Default: yes | ||
| ahf_mask_2 | Scope: private | BOOLEAN |
| Description: Mask for third horizon with find3?
| ||
| Default: yes | ||
| ahf_mask_time | Scope: private | REAL |
| Description: Time after which to start setting the mask
| ||
| Range | Default: -1.0 | |
| :
| Anything goes. Negative number means setting the mask as soon as
possible
| |
| ahf_maskbuffer | Scope: private | INT |
| Description: Number of grid points in mask buffer zone
| ||
| Range | Default: 5 | |
| 0:* | Positive please
| |
| ahf_maskshrink | Scope: private | REAL |
| Description: Shrink factor for mask
| ||
| Range | Default: 0.8 | |
| 0.0:1.0 | Must be positive and not larger than 1
| |
| ahf_masktype | Scope: private | KEYWORD |
| Description: Type of mask
| ||
| Range | Default: cube | |
| lego | Mask is a lego sphere
| |
| cube | Mask is a cube
| |
| poly | Mask is a polyhedra
| |
| ahf_maxchange | Scope: private | REAL |
| Description: Maximum relative difference between 1 big and 2 small steps
| ||
| Range | Default: 0.1 | |
| : | Anything
| |
| ahf_maxiter | Scope: private | INT |
| Description: Maximum number of iterations of POWELL
| ||
| Range | Default: 10 | |
| : | Any sensible integer value
| |
| ahf_minarea | Scope: private | BOOLEAN |
| Description: Minimize area instead of expansion?
| ||
| Default: no | ||
| ahf_minchange | Scope: private | REAL |
| Description: Minimum relative difference between 1 big and 2 small steps
| ||
| Range | Default: 0.01 | |
| : | Anything
| |
| ahf_nn0 | Scope: private | INT |
| Description: Number of subdivisions of c0(0) for initial guess
| ||
| Range | Default: 10 | |
| : | Some positive integer
| |
| ahf_nn2 | Scope: private | INT |
| Description: Number of subdivisions of c0(2) for initial guess
| ||
| Range | Default: 10 | |
| : | Some positive integer
| |
| ahf_nphi | Scope: private | INT |
| Description: Number of subdivisions in phi
| ||
| Range | Default: 100 | |
| 1: | Any sensible integer
| |
| ahf_ntheta | Scope: private | INT |
| Description: Number of subdivisions in theta
| ||
| Range | Default: 100 | |
| 1: | Any sensible integer
| |
| ahf_octant | Scope: private | KEYWORD |
| Description: Octant symmetry?
| ||
| Range | Default: no | |
| no | No octant symmetry
| |
| yes | Octant symmetry: reflection symmetry on all three coordinate planes
| |
| high | Octant symmetry + symmetry of rotation of pi/2 around z axis
| |
| ahf_offset | Scope: private | BOOLEAN |
| Description: Center offset from origin?
| ||
| Default: no | ||
| ahf_phi | Scope: private | BOOLEAN |
| Description: Expand also in phi? (seach for non-axisymmetric surface)
| ||
| Default: no | ||
| ahf_r0 | Scope: private | REAL |
| Description: Radius of initial sphere (0 forces largest sphere)
| ||
| Range | Default: 0.0 | |
| : | Anything
| |
| ahf_r0_0 | Scope: private | REAL |
| Description: Radius of first initial sphere for find3 (0 forces largest sphere)
| ||
| Range | Default: 0.0 | |
| : | Anything
| |
| ahf_r0_1 | Scope: private | REAL |
| Description: Radius of second initial sphere for find3 (0 forces largest sphere)
| ||
| Range | Default: 0.0 | |
| : | Anything
| |
| ahf_r0_2 | Scope: private | REAL |
| Description: Radius of third initial sphere for find3 (0 forces largest sphere)
| ||
| Range | Default: 0.0 | |
| : | Anything
| |
| ahf_refx | Scope: private | BOOLEAN |
| Description: Reflection symmetry x->-x?
| ||
| Default: no | ||
| ahf_refy | Scope: private | BOOLEAN |
| Description: Reflection symmetry y->-y?
| ||
| Default: no | ||
| ahf_refz | Scope: private | BOOLEAN |
| Description: Reflection symmetry z->-z?
| ||
| Default: no | ||
| ahf_reportalways | Scope: private | BOOLEAN |
| Description: Report for all surfaces found (yes) or just for apparent horizons (no)
| ||
| Default: no | ||
| ahf_shiftcoeff | Scope: private | REAL |
| Description: Coefficient for shift
| ||
| Range | Default: 0.0 | |
| : | Anything goes
| |
| ahf_sloppyguess | Scope: private | BOOLEAN |
| Description: Use sphere as initial guess?
| ||
| Default: no | ||
| ahf_tol | Scope: private | REAL |
| Description: Tolerance for minimization routines
| ||
| Range | Default: 0.1 | |
| 0: | A sensible positive number
| |
| ahf_trapped_surface | Scope: private | BOOLEAN |
| Description: Minimize (expansion + delta) to find trapped surface?
| ||
| Default: no | ||
| ahf_verbose | Scope: private | BOOLEAN |
| Description: Print messages to screen?
| ||
| Default: yes | ||
| ahf_veryverbose | Scope: private | BOOLEAN |
| Description: Print messages at each iteration step to screen?
| ||
| Default: no | ||
| ahf_wander | Scope: private | BOOLEAN |
| Description: Allow the center to wander?
| ||
| Default: no | ||
| ahf_xc | Scope: private | REAL |
| Description: x-coordinate of center of expansion
| ||
| Range | Default: 0.0 | |
| : | Anything
| |
| ahf_xc_0 | Scope: private | REAL |
| Description: x-coordinate of center of expansion for first surface with find3
| ||
| Range | Default: 0.0 | |
| : | Anything
| |
| ahf_xc_1 | Scope: private | REAL |
| Description: x-coordinate of center of expansion for second surface with find3
| ||
| Range | Default: 0.0 | |
| : | Anything
| |
| ahf_xc_2 | Scope: private | REAL |
| Description: x-coordinate of center of expansion for third surface with find3
| ||
| Range | Default: 0.0 | |
| : | Anything
| |
| ahf_yc | Scope: private | REAL |
| Description: y-coordinate of center of expansion
| ||
| Range | Default: 0.0 | |
| : | Anything
| |
| ahf_yc_0 | Scope: private | REAL |
| Description: y-coordinate of center of expansion for first surface with find3
| ||
| Range | Default: 0.0 | |
| : | Anything
| |
| ahf_yc_1 | Scope: private | REAL |
| Description: y-coordinate of center of expansion for second surface with find3
| ||
| Range | Default: 0.0 | |
| : | Anything
| |
| ahf_yc_2 | Scope: private | REAL |
| Description: y-coordinate of center of expansion for third surface with find3
| ||
| Range | Default: 0.0 | |
| : | Anything
| |
| ahf_zc | Scope: private | REAL |
| Description: z-coordinate of center of expansion
| ||
| Range | Default: 0.0 | |
| : | Anything
| |
| ahf_zc_0 | Scope: private | REAL |
| Description: z-coordinate of center of expansion for first surface with find3
| ||
| Range | Default: 0.0 | |
| : | Anything
| |
| ahf_zc_1 | Scope: private | REAL |
| Description: z-coordinate of center of expansion for second surface with find3
| ||
| Range | Default: 0.0 | |
| : | Anything
| |
| ahf_zc_2 | Scope: private | REAL |
| Description: z-coordinate of center of expansion for third surface with find3
| ||
| Range | Default: 0.0 | |
| : | Anything
| |
| horizon_to_announce_centroid | Scope: private | INT |
| Description: For which horizon should we announce the centroid to driftcorrect
| ||
| Range | Default: (none) | |
| don’t announce the centroid
| ||
| 1:3 | announce this horizon’s centroid each time we find it
| |
| horizon_to_output_centroid | Scope: private | INT |
| Description: For which horizon should we output the centroid
| ||
| Range | Default: (none) | |
| don’t output any centroids
| ||
| 1:3 | output this horizon’s centroid each time we find it
| |
| interpolation_operator | Scope: private | STRING |
| Description: Name of interpolation operator to use
| ||
| Range | Default: uniform cartesian | |
| .+ | A valid name for a registered interpolation operator
| |
| interpolation_order | Scope: private | INT |
| Description: Order for interpolation
| ||
| Range | Default: 2 | |
| 1:4 | Choose between first and fourth order interpolation
| |
| trapped_surface_delta | Scope: private | REAL |
| Description: find (expansion = delta) surface
| ||
| Range | Default: 0.0 | |
| : | Just a real number
| |
| ahf_active | Scope: restricted | BOOLEAN |
| Description: Activate AHFinder?
| ||
| Default: no | ||
| ahf_persists | Scope: restricted | BOOLEAN |
| Description: Do the finder grid functions stay around?
| ||
| Default: no | ||
| use_mask | Scope: shared from SPACEMASK | BOOLEAN |
Implements:
ahfinder
Inherits:
admbase
staticconformal
spacemask
grid
io
admmacros
| Group Names | Variable Names | Details | |
| triggergroup | compact | 0 | |
| triggervar | description | For triggering output | |
| dimensions | 0 | ||
| distribution | CONSTANT | ||
| group type | SCALAR | ||
| timelevels | 1 | ||
| variable type | INT | ||
| ahfgradient | compact | 0 | |
| ahfgradx | description | Grid functions for gradients | |
| ahfgrady | dimensions | 3 | |
| ahfgradz | distribution | DEFAULT | |
| ahfgradn | group type | GF | |
| timelevels | 1 | ||
| variable type | REAL | ||
| ahfinder_gauss | compact | 0 | |
| ahfgauss | description | Grid function for gaussian curvature calculation | |
| dimensions | 3 | ||
| distribution | DEFAULT | ||
| group type | GF | ||
| timelevels | 1 | ||
| variable type | REAL | ||
| find3grid | compact | 0 | |
| ahfgrid3 | description | Grid functions to use in find3 algorithm | |
| ahf_exp3 | dimensions | 3 | |
| distribution | DEFAULT | ||
| group type | GF | ||
| timelevels | 1 | ||
| variable type | REAL | ||
| ahf_centroid | compact | 0 | |
| ahf_centroid_x | description | Centroid of one of the horizons | |
| ahf_centroid_y | dimensions | 0 | |
| ahf_centroid_z | distribution | CONSTANT | |
| group type | SCALAR | ||
| timelevels | 1 | ||
| variable type | REAL | ||
| drift_check | compact | 0 | |
| drift_first | description | For checking if its the first drift correction | |
| dimensions | 0 | ||
| distribution | CONSTANT | ||
| group type | SCALAR | ||
| timelevels | 1 | ||
| variable type | INT | ||
| Group Names | Variable Names | Details | |
| out_scalars | compact | 0 | |
| out_mass | description | Output of scalar variables | |
| out_radius | dimensions | 0 | |
| out_area | distribution | CONSTANT | |
| out_perimeter | group type | SCALAR | |
| out_meridian1 | timelevels | 1 | |
| out_meridian2 | variable type | REAL | |
| out_1d_legen | compact | 0 | |
| out_c0 | description | Output of c0 coefficients | |
| dimensions | 1 | ||
| distribution | CONSTANT | ||
| group type | ARRAY | ||
| size | AHF_LMAX | ||
| timelevels | 1 | ||
| variable type | REAL | ||
| out_2d_legen | compact | 0 | |
| out_cc | description | Output of cc and cs coefficients | |
| out_cs | dimensions | 2 | |
| distribution | CONSTANT | ||
| group type | ARRAY | ||
| size | AHF_LMAX | ||
| size | AHF_LMAX | ||
| timelevels | 1 | ||
| variable type | REAL | ||
| ahfinder_gaussian | compact | 0 | |
| gaussian | description | Gaussian Curvature | |
| dimensions | 2 | ||
| distribution | CONSTANT | ||
| group type | ARRAY | ||
| size | AHF_NTHETA+1 | ||
| size | AHF_NPHI+1 | ||
| timelevels | 1 | ||
| variable type | REAL | ||
| Group Names | Variable Names | Details | |
| ahfindergrid | compact | 0 | |
| ahfgrid | description | Horizon function | |
| dimensions | 3 | ||
| distribution | DEFAULT | ||
| group type | GF | ||
| timelevels | 1 | ||
| variable type | REAL | ||
| ahfinderexp | compact | 0 | |
| ahf_exp | description | Expansion | |
| dimensions | 3 | ||
| distribution | DEFAULT | ||
| group type | GF | ||
| timelevels | 1 | ||
| variable type | REAL | ||
| ahfmask | compact | 0 | |
| ahmask | description | Grid function for masking | |
| dimensions | 3 | ||
| distribution | DEFAULT | ||
| group type | GF | ||
| timelevels | 1 | ||
| variable type | REAL | ||
| hole1_bounds | compact | 0 | |
| dhole1_xmin | description | Bounds of excision box for hole 1 | |
| dhole1_ymin | dimensions | 0 | |
| dhole1_zmin | distribution | CONSTANT | |
| dhole1_xmax | group type | SCALAR | |
| dhole1_ymax | timelevels | 1 | |
| dhole1_zmax | variable type | REAL | |
| hole2_bounds | compact | 0 | |
| dhole2_xmin | description | Bounds of excision box for hole 2 | |
| dhole2_ymin | dimensions | 0 | |
| dhole2_zmin | distribution | CONSTANT | |
| dhole2_xmax | group type | SCALAR | |
| dhole2_ymax | timelevels | 1 | |
| dhole2_zmax | variable type | REAL | |
| hole3_bounds | compact | 0 | |
| dhole3_xmin | description | Bounds of excision box for hole 3 | |
| dhole3_ymin | dimensions | 0 | |
| dhole3_zmin | distribution | CONSTANT | |
| dhole3_xmax | group type | SCALAR | |
| dhole3_ymax | timelevels | 1 | |
| dhole3_zmax | variable type | REAL | |
This section lists all the variables which are assigned storage by thorn EinsteinAnalysis/AHFinder. Storage can either last for the duration of the run (Always means that if this thorn is activated storage will be assigned, Conditional means that if this thorn is activated storage will be assigned for the duration of the run if some condition is met), or can be turned on for the duration of a schedule function.
| Conditional: | |
| hole1_bounds hole2_bounds hole3_bounds ahf_centroid | |
| out_scalars | |
| ahfinder_gaussian | |
| out_1d_legen out_2d_legen | |
| ahfindergrid ahfinderexp ahfgradient ahfinder_gauss find3grid | |
| ahfmask | |
| ahfmask | |
| hole1_bounds hole2_bounds hole3_bounds | |
CCTK_WRAGH
ahfinder_setsym
set symmetries for ahfinder grid functions
| Language: | fortran | |
| Options: | global | |
| Type: | function | |
CCTK_STARTUP
ahfinder_startup
register ahfinder as an io method
| Language: | c | |
| Options: | global | |
| Type: | function | |
CCTK_PARAMCHECK
ahfinder_paramcheck
check for physical or conformal metric
| Language: | fortran | |
| Options: | global | |
| Type: | function | |
CCTK_INITIAL
ahfinder_initoutput
create output files, write headers
| Language: | fortran | |
| Type: | function | |
CCTK_ANALYSIS (conditional)
ahfinder
call apparent horizon finder with persisting grid functions
| Before: | driftcorrect | |
| Language: | fortran | |
| Storage: | triggergroup | |
| Triggers: | triggergroup | |
| Type: | function | |
CCTK_ANALYSIS (conditional)
ahfinder
call apparent horizon finder
| Before: | driftcorrect | |
| Language: | fortran | |
| Storage: | ahfindergrid | |
| ahfinderexp | ||
| ahfgradient | ||
| ahfinder_gauss | ||
| find3grid | ||
| ahfmask | ||
| triggergroup | ||
| Triggers: | triggergroup | |
| Type: | function | |
CCTK_ANALYSIS (conditional)
ahfinder
call apparent horizon finder with persisting mask
| Before: | driftcorrect | |
| Language: | fortran | |
| Storage: | ahfindergrid | |
| ahfinderexp | ||
| ahfgradient | ||
| ahfinder_gauss | ||
| find3grid | ||
| triggergroup | ||
| Triggers: | triggergroup | |
| Type: | function | |